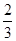题目内容
在正项数列 中,
中, .对任意的
.对任意的 ,函数
,函数


 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
 中,
中, .对任意的
.对任意的 ,函数
,函数


 满足
满足 .
.(1)求数列
 的通项公式;
的通项公式;(2)求数列
 的前
的前 项和
项和 .
.(1)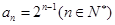 ;(2)
;(2)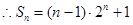 .
.
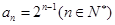 ;(2)
;(2)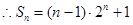 .
.试题分析:本题主要考查导数的运算、等比数列的证明、等比数列的通项公式、等比数列的前n项和公式、错位相减法等基础知识,考查学生的化归与转化能力和运算能力.第一问,先利用
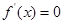 得到一个递推公式,根据等比数列的证明方法知数列
得到一个递推公式,根据等比数列的证明方法知数列 为等比数列,则利用等比数列的通项公式求基本量
为等比数列,则利用等比数列的通项公式求基本量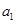 和
和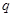 ,从而求出通过公式;2.先求出
,从而求出通过公式;2.先求出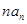 的表达式,根据式子的规律,符合错位相减法,利用错位相减法和等比数列的前n项和求出
的表达式,根据式子的规律,符合错位相减法,利用错位相减法和等比数列的前n项和求出 .
.试题解析:(1)求导得
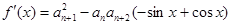 ,由
,由 可得
可得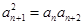 ,又
,又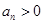 ,故数列
,故数列 为等比数列,且公比
为等比数列,且公比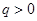 . 3分
. 3分由
 得
得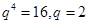 ,所以通项公式为
,所以通项公式为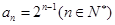 . 6分
. 6分(2)
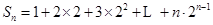 ①
①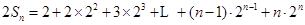 ②
②①-②得,
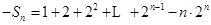
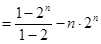
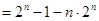
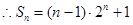 12分
12分
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
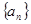 中,
中,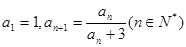
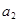 ,
,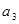 ;
;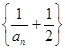 是等比数列,并求
是等比数列,并求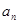 ;
;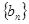 满足
满足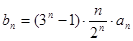 ,数列
,数列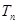 ,若不等式
,若不等式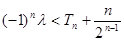 对一切
对一切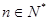 恒成立,求
恒成立,求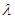 的取值范围.
的取值范围.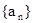 中,
中,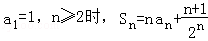
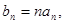 求数列
求数列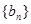 的前n项和Tn.
的前n项和Tn.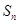 是等比数列{an}的前n项和,
是等比数列{an}的前n项和,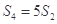 ,则
,则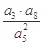 的值为( )
的值为( ) 或-1
或-1


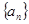 中,
中,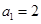 ,
,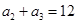 ,则该数列的前4项和为 .
,则该数列的前4项和为 .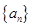 的前
的前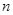 项和为
项和为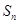 ,则下列一定成立的是( )
,则下列一定成立的是( ) ,则
,则
 ,则
,则


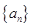 满足
满足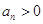 ,
,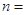 l,2,…,且
l,2,…,且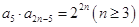 ,则当
,则当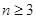 时,
时, 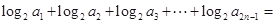 ____________.
____________. 的前
的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列,则数列
成等差数列,则数列
 等于( )
等于( )