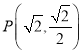题目内容
【题目】已知椭圆![]() 的一个焦点与短轴的两端点组成一个正三角形的三个顶点,且椭圆经过点
的一个焦点与短轴的两端点组成一个正三角形的三个顶点,且椭圆经过点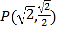 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以线段
两点,且以线段![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设椭圆的上下顶点为![]() ,
,![]() ,左焦点为
,左焦点为![]() ,则
,则![]() 是正三角形,可得
是正三角形,可得![]() ,进而将
,进而将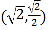 代入椭圆方程,可求出
代入椭圆方程,可求出![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,并消去
,与椭圆方程联立,并消去![]() 得到关于
得到关于![]() 的一元二次方程,设
的一元二次方程,设![]() ,
,![]() ,由以线段
,由以线段![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,可得
,可得![]() ,将其展开并结合韦达定理,可求得
,将其展开并结合韦达定理,可求得![]() ,即直线
,即直线![]() 恒过点
恒过点![]() ,进而
,进而![]() ,结合韦达定理,求出最大值即可.
,结合韦达定理,求出最大值即可.
(1)根据题意,设椭圆的上下顶点为![]() ,
,![]() ,左焦点为
,左焦点为![]() ,
,
则![]() 是正三角形,所以
是正三角形,所以![]() ,则椭圆方程为
,则椭圆方程为![]() .
.
将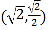 代入椭圆方程,可得
代入椭圆方程,可得![]() ,解得
,解得![]() ,
,![]() .
.
故椭圆的方程为![]() .
.
(2)由题意,设直线![]() 的方程为
的方程为![]() ,
,
联立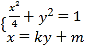 ,消去
,消去![]() 得
得![]() .
.
设![]() ,
,![]() ,则有
,则有![]() ,
,![]() ,
,
因为以线段![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,所以
,所以![]() ,
,
由![]() ,
,![]() ,则
,则![]() ,
,
将![]() ,
,![]() 代入上式并整理得
代入上式并整理得![]() ,
,
则![]() ,化简得
,化简得![]() ,
,
解得![]() 或
或![]() ,
,
因为直线![]() 不过点
不过点![]() ,所以
,所以![]() ,故
,故![]() .
.
所以直线![]() 恒过点
恒过点![]() .
.
故![]()
 ,
,
设![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,
所以![]() 面积的最大值为
面积的最大值为![]() .
.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】某企业为了参加上海的进博会,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
已知![]() .参考公式:
.参考公式: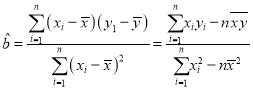 ,
,![]()
(1)求出q的值;
(2)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程![]() ;
;
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有一个是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有一个是“好数据”的概率.
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.