题目内容
【题目】已知F1 ， F2为椭圆C： 
（a＞b＞0）的左、右焦点，M为椭圆C的上顶点，且|MF1|=2，右焦点与右顶点的距离为1．
（1）求椭圆C的标准方程；
（2）若直线l与椭圆C相交于A，B两点，且直线OA，OB的斜率kOA ， kOB满足kOAkOB=﹣ 
，求△AOB的面积．
【答案】
（1）解：由题意得，a=2，a﹣c=1，得c=1，a2=b2+c2，
∴b2=3，
∴椭圆的方程为 
（2）解：①当直线l的斜率不存在时，设l：x=n，不妨取A（n， 
），B（n，﹣ ），
由kOAkOB=﹣ 
，解得n2=2．
此时，S△AOB= 
丨AB丨丨n丨= 
，
②当直线l的斜率存在时，设l：y=kx+m，A（x1，y1），B（x2，y2），
由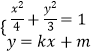 
，消去y化简得：（3+4k2）x2+8kmx+4m2﹣12=0，
由韦达定理可知x1+x2=﹣ 
，x1x2= 
，△＞0得4k2﹣m2+3＞0
kOAkOB=﹣ ， 
=﹣ ，即：3x1x2+4y1y2=0，
即：3x1x2+4（kx1+m）（kx2+m）=0，
即：（3+4k2）x1x2+4km（x1+m2）+4m2=0，
化简整理得：3+4k2=2m2，
由弦长公式得：丨AB丨= 
，
= 
，
O到直线y=kx+m的距离d= 
，则：
S△AOB= 丨AB丨d= 
丨m丨，
= 
丨m丨，
= ．
综上所述，S△/span>AOB=
【解析】（1）由椭圆的性质，|MF1|=2，即a=2，a﹣c=1，即可求得c=1，b2=3，即可求得椭圆的方程；（2）当直线l斜率不存在时，kOAkOB=﹣ ，求得A和B点坐标，利用三角形面积公式，即可求得△AOB的面积，当直线l的斜率存在，设出直线l的方程，将直线l的方程代入椭圆方程，消去y得到关于x的一元二次方程，根据韦达定理求得x1+x2和x1x2 ， 根据斜率公式求得表示出kOAkOB ， 由点到直线距离公式及三角形面积公式，即可求得△AOB的面积，综上即可求得△AOB的面积．
