题目内容
有10双互不相同的鞋子混装在一只口袋中,从中任意取出4只,试求出现以下结果时各有多少种情况?
(1)4只鞋子恰成两双;
(2)4只鞋子没有成双的.
(1)4只鞋子恰成两双;
(2)4只鞋子没有成双的.
(1)45;(2)3360.
第一问中利用古典概型概率公式可知,只需选出两双鞋,所以有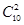 =45(种)情况.
=45(种)情况.
第二问中,利用4只鞋若没有成双的,则它们来自于4双鞋;先从10双中取4双,有C种取法,再从每双中取一只,各有C种取法,所以由分步乘法计数原理共有
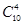 ·
·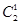
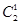
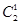
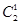 =3 360(种)情况
=3 360(种)情况
解: (1)根据题意只需选出两双鞋,所以有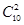 =45(种)情况.
=45(种)情况.
(2)方法一:4只鞋若没有成双的,则它们来自于4双鞋;先从10双中取4双,有C种取法,再从每双中取一只,各有C种取法,所以由分步乘法计数原理共有
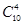 ·
·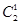
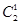
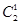
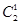 =3 360(种)情况.
=3 360(种)情况.
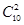 =45(种)情况.
=45(种)情况.第二问中,利用4只鞋若没有成双的,则它们来自于4双鞋;先从10双中取4双,有C种取法,再从每双中取一只,各有C种取法,所以由分步乘法计数原理共有
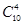 ·
·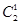
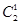
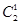
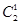 =3 360(种)情况
=3 360(种)情况解: (1)根据题意只需选出两双鞋,所以有
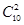 =45(种)情况.
=45(种)情况.(2)方法一:4只鞋若没有成双的,则它们来自于4双鞋;先从10双中取4双,有C种取法,再从每双中取一只,各有C种取法,所以由分步乘法计数原理共有
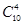 ·
·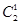
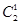
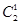
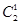 =3 360(种)情况.
=3 360(种)情况.
练习册系列答案
相关题目

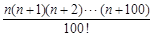 可表示为( )
可表示为( )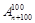
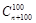
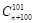
 = .
= .