题目内容
设函数 .
.
(1)当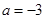 ,
,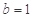 时,求函数
时,求函数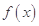 的最大值;
的最大值;
(2)令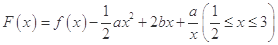 ,其图象上存在一点
,其图象上存在一点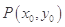 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数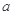 的取值范围;
的取值范围;
(3)当 ,
,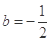 时,方程
时,方程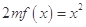 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.
 .
.(1)当
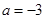 ,
,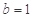 时,求函数
时,求函数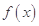 的最大值;
的最大值;(2)令
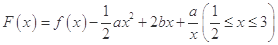 ,其图象上存在一点
,其图象上存在一点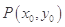 ,使此处切线的斜率
,使此处切线的斜率 ,求实数
,求实数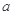 的取值范围;
的取值范围;(3)当
 ,
,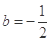 时,方程
时,方程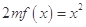 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.(1)函数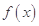 的最大值为
的最大值为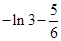 ;(2)实数
;(2)实数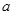 的取值范围是
的取值范围是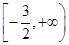 ;(3)
;(3) .
.
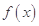 的最大值为
的最大值为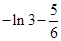 ;(2)实数
;(2)实数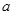 的取值范围是
的取值范围是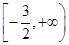 ;(3)
;(3) .
.试题分析:(1)将
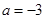 ,
, 代入函数
代入函数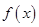 的解析式,然后利用导数求出函数
的解析式,然后利用导数求出函数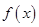 的最大值;(2)先确定函数
的最大值;(2)先确定函数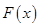 的解析式,并求出函数
的解析式,并求出函数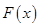 的导数,然后利用导数的几何意义将问题转化为
的导数,然后利用导数的几何意义将问题转化为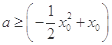 ,利用恒成立的思想进行求解;(3)方法一是利用参数分离,将问题转化为方程
,利用恒成立的思想进行求解;(3)方法一是利用参数分离,将问题转化为方程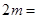 、
、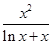 有且仅有一个实根,然后构造新函数
有且仅有一个实根,然后构造新函数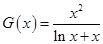 ,利用导数求出函数
,利用导数求出函数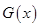 的极值从而求出参数
的极值从而求出参数 的值;方法二是直接构造新函数
的值;方法二是直接构造新函数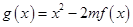 ,利用导数求函数
,利用导数求函数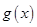 的极值,并对参数
的极值,并对参数 的取值进行分类讨论,从而求出参数
的取值进行分类讨论,从而求出参数 的值.
的值.试题解析:(1)依题意,
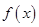 的定义域为
的定义域为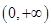 ,
,当
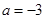 ,
, 时,
时,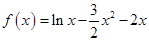 ,
,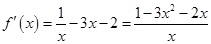 ,
,由
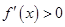 ,得
,得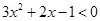 ,解得
,解得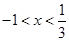 ;
;由
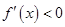 ,得
,得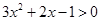 ,解得
,解得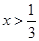 或
或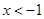 .
.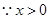 ,
,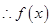 在
在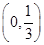 单调递增,在
单调递增,在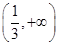 单调递减;
单调递减; 所以
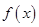 的极大值为
的极大值为 ,此即为最大值;
,此即为最大值;(2)
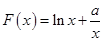 ,
,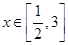 ,则有
,则有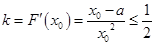 在
在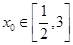 上有解,
上有解,∴
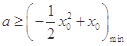 ,
,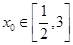
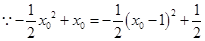 ,
,所以当
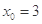 时,
时,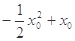 取得最小值
取得最小值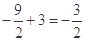 ,
,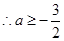 ;
;(3)方法1:由
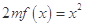 得
得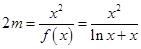 ,令
,令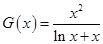 ,
,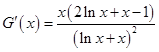 ,
,令
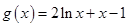 ,
,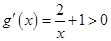 ,∴
,∴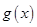 在
在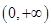 单调递增,
单调递增, 而
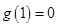 ,∴在
,∴在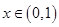 ,
,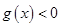 ,即
,即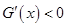 ,在
,在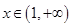 ,
,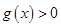 ,即
,即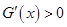 ,
,∴
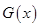 在
在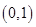 单调递减,在
单调递减,在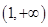 单调递增,
单调递增, ∴
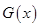 极小值为
极小值为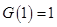 ,令
,令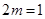 ,即
,即 时方程
时方程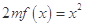 有唯一实数解.
有唯一实数解. 方法2:因为方程
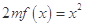 有唯一实数解,所以
有唯一实数解,所以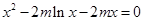 有唯一实数解,
有唯一实数解,设
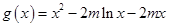 ,则
,则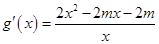 ,令
,令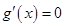 ,
,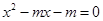 因为
因为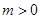 ,
,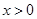 ,所以
,所以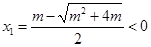 (舍去),
(舍去),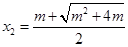 ,
,当
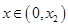 时,
时,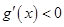 ,
,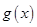 在
在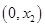 上单调递减,
上单调递减,当
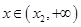 时,
时,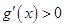 ,
,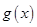 在
在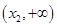 上单调递增,
上单调递增, 当
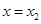 时,
时,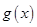 取最小值
取最小值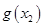 .
. 若方程
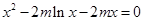 有唯一实数解,
有唯一实数解,则必有
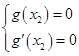 即
即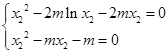
所以
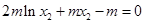 ,因为
,因为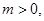 所以
所以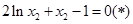 12分
12分设函数
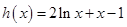 ,因为当
,因为当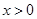 时,
时,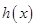 是增函数,所以
是增函数,所以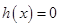 至多有一解.
至多有一解.∵
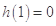 ,∴方程(*)的解为
,∴方程(*)的解为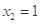 ,即
,即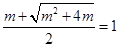 ,解得
,解得 .
.
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
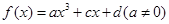 是R上的奇函数,当
是R上的奇函数,当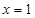 时
时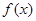 取得极值
取得极值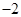 .
.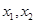
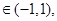 不等式
不等式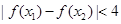 恒成立.
恒成立.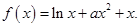
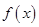 在
在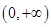 是增函数,求
是增函数,求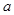 的取值范围;
的取值范围;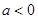 ,对于函数
,对于函数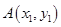 ,
,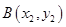 ,其中
,其中 ,直线
,直线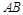 的斜率为
的斜率为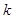 ,记
,记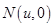 ,若
,若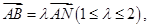 求证:
求证: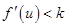 .
.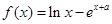 .
.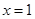 是,
是,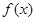 的极值点,讨论
的极值点,讨论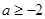 时,证明:
时,证明: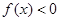 .
.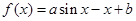 (
(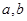 均为正常数),设函数
均为正常数),设函数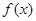 在
在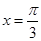 处有极值.
处有极值.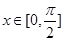 ,不等式
,不等式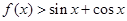 总成立,求实数
总成立,求实数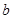 的取值范围;
的取值范围;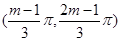 上单调递增,求实数
上单调递增,求实数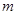 的取值范围.
的取值范围. .
. 的单调区间和极值;
的单调区间和极值; 直线
直线 与曲线
与曲线 相交于
相交于 不同两点,若
不同两点,若 试证明
试证明 .
. ,函数
,函数 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最小值.
上的最小值. ,
, 的图象经过
的图象经过 和
和 两点,如图所示,且函数
两点,如图所示,且函数 的值域为
的值域为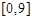 .过该函数图象上的动点
.过该函数图象上的动点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接 .
.
 的面积为
的面积为 ,求
,求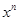 +
+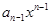 +
+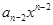 +…+
+…+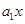 +
+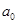 (n>2且n∈N﹡)设
(n>2且n∈N﹡)设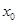 是函数f(x)的零点的最大值,则下述论断一定错误的是( )
是函数f(x)的零点的最大值,则下述论断一定错误的是( )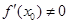
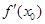 =0
=0