题目内容
已知函数f(x)=sin(ωx+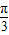 )(x∈R),且
)(x∈R),且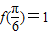 .
.(1)求ω的最小正值及此时函数y=f(x)的表达式;
(2)将(1)中所得函数y=f(x)的图象结果怎样的变换可得
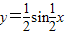 的图象;
的图象;(3)在(1)的前提下,设
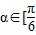 ,
,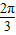 ,
,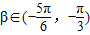 ,
,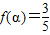 ,f(β)=-
,f(β)=- ,
,①求tanα的值;
②求cos2(α-β)-1的值.
【答案】分析:(1)将x用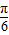 代替,求出正弦为1的所有角,求出其中的最小值.
代替,求出正弦为1的所有角,求出其中的最小值.
(2)据图象的平移规律:左加右减;伸缩变换的规律:横坐标变为自变量x的乘的数的倒数;若三角函数符号前乘的数为A,则纵坐标变为原来的A倍.
(3)利用三角函数的平方关系求出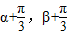 的余弦,利用商数关系求出
的余弦,利用商数关系求出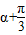 的正切;由于
的正切;由于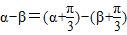
利用两角和的正弦公式求出sin(α-β),再利用二倍角公式求出值.
解答:解:(1)因为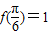 ,所以
,所以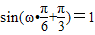 ,
,
于是ω•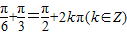 ,即ω=1+12k(k∈Z),
,即ω=1+12k(k∈Z),
故当k=0时,ω取得最小正值1.
此时 .
.
(2)先将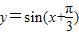 的图象向右平移
的图象向右平移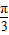 个单位得y=sinx的图象;
个单位得y=sinx的图象;
再将所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变)得y=sin x的图象;
x的图象;
最后将所得图象上各点的纵坐标缩小到原来的 倍(横坐标不变)得y=
倍(横坐标不变)得y=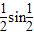 x的图象.
x的图象.
(3)因为f(α)=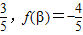 ,
,
所以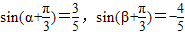 .
.
因为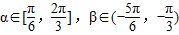 ,
,
所以α+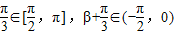 .
.
于是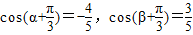 .
.
①因为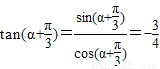 ,
,
所以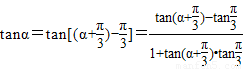 =
= .
.
②因为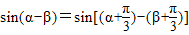 =
=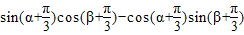 =
=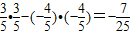 ,
,
所以cos2(α-β)-1=-2sin2(α-β)=-2×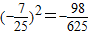 .
.
点评:本题考查三角函数的图象变换规律,三角函数的同角三角函数的公式,三角函数的二倍角公式.
将未知的角用已知的角表示,从而将未知的三角函数用已知的三角函数表示.
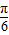 代替,求出正弦为1的所有角,求出其中的最小值.
代替,求出正弦为1的所有角,求出其中的最小值.(2)据图象的平移规律:左加右减;伸缩变换的规律:横坐标变为自变量x的乘的数的倒数;若三角函数符号前乘的数为A,则纵坐标变为原来的A倍.
(3)利用三角函数的平方关系求出
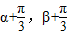 的余弦,利用商数关系求出
的余弦,利用商数关系求出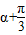 的正切;由于
的正切;由于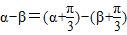
利用两角和的正弦公式求出sin(α-β),再利用二倍角公式求出值.
解答:解:(1)因为
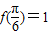 ,所以
,所以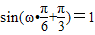 ,
,于是ω•
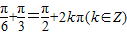 ,即ω=1+12k(k∈Z),
,即ω=1+12k(k∈Z),故当k=0时,ω取得最小正值1.
此时
 .
.(2)先将
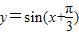 的图象向右平移
的图象向右平移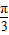 个单位得y=sinx的图象;
个单位得y=sinx的图象;再将所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变)得y=sin
 x的图象;
x的图象;最后将所得图象上各点的纵坐标缩小到原来的
 倍(横坐标不变)得y=
倍(横坐标不变)得y=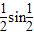 x的图象.
x的图象.(3)因为f(α)=
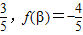 ,
,所以
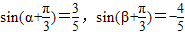 .
.因为
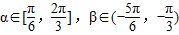 ,
,所以α+
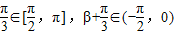 .
.于是
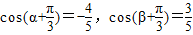 .
.①因为
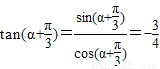 ,
,所以
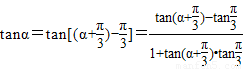 =
= .
.②因为
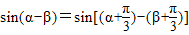 =
=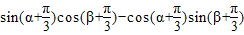 =
=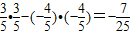 ,
,所以cos2(α-β)-1=-2sin2(α-β)=-2×
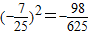 .
.点评:本题考查三角函数的图象变换规律,三角函数的同角三角函数的公式,三角函数的二倍角公式.
将未知的角用已知的角表示,从而将未知的三角函数用已知的三角函数表示.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
