题目内容
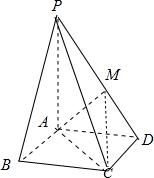 如图,四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,PA=2
如图,四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,PA=2| 3 |
(Ⅰ)证明:平面ACM⊥平面PCD;
(Ⅱ)求三棱锥M-PAC的高.
考点:平面与平面垂直的判定,棱锥的结构特征
专题:证明题,空间位置关系与距离
分析:(Ⅰ)先证明CD⊥AM,由AM⊥平面PCD,即可证明平面ACM⊥平面PCD;
(Ⅱ)先证明AM为三棱锥M-PAC的高,可求得∠DPA=30°,从而有AM=
PA=
.
(Ⅱ)先证明AM为三棱锥M-PAC的高,可求得∠DPA=30°,从而有AM=
| 1 |
| 2 |
| 3 |
解答:
证明:(Ⅰ)∵四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,
∴CD⊥AD,CD⊥AP
∵AD∩AP=P
∴CD⊥平面PAD
∵CM?平面PAD
∴CD⊥AM
∵AM⊥PD,CD∩PD=D
∴AM⊥平面PCD
∵AM?平面ACM
∴平面ACM⊥平面PCD;
(Ⅱ)由(Ⅰ)已证明CD⊥AM,AM⊥PD
∴AM⊥PC
∴AM为三棱锥M-PAC的高.
∵PA=2
,AB=1,AD=2,
∴PD=4,∠DPA=30°,
∴AM=
PA=
.
∴三棱锥M-PAC的高为
.
∴CD⊥AD,CD⊥AP
∵AD∩AP=P
∴CD⊥平面PAD
∵CM?平面PAD
∴CD⊥AM
∵AM⊥PD,CD∩PD=D
∴AM⊥平面PCD
∵AM?平面ACM
∴平面ACM⊥平面PCD;
(Ⅱ)由(Ⅰ)已证明CD⊥AM,AM⊥PD
∴AM⊥PC
∴AM为三棱锥M-PAC的高.
∵PA=2
| 3 |
∴PD=4,∠DPA=30°,
∴AM=
| 1 |
| 2 |
| 3 |
∴三棱锥M-PAC的高为
| 3 |
点评:本题主要考察了平面与平面垂直的判定,棱锥的结构特征,属于基本知识的考查.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知等比数列{an}中,a3,a7是一元二次方程x2+7x+9=0的两根,则a5=( )
| A、3 | B、-3 | C、±3 | D、9 |
已知函数f(x)=
,那么f[f(-2)]=( )
|
| A、-16 | B、16 | C、2 | D、-2 |
 如图,在三棱锥A-BCD中,AB=CD=6,AC=BD=8,BC=10,且A在平面BCD上的投影O恰好在BD上.
如图,在三棱锥A-BCD中,AB=CD=6,AC=BD=8,BC=10,且A在平面BCD上的投影O恰好在BD上.