题目内容
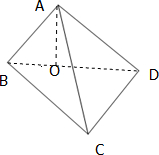
 如图,在三棱锥A-BCD中,AB=CD=6,AC=BD=8,BC=10,且A在平面BCD上的投影O恰好在BD上.
如图,在三棱锥A-BCD中,AB=CD=6,AC=BD=8,BC=10,且A在平面BCD上的投影O恰好在BD上.(1)求证:AB⊥CD;
(2)求证:AB⊥面ACD;
(3)求三棱锥A-BCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知中A在平面BCD上的投影O恰好在BD上,可得平面ABD⊥平面BCD,进而由勾股定理可得CD⊥BD,则CD⊥平面ABD,最后AB⊥CD;
(2)由勾股定理可得AB⊥AC,结合(1)中结论及线面垂直的判定定理可得AB⊥面ACD;
(3)根据(2)可得AB⊥AD,由勾股定理和等积法,求出AO的长,即棱锥的高,进而可得三棱锥A-BCD的体积.
(2)由勾股定理可得AB⊥AC,结合(1)中结论及线面垂直的判定定理可得AB⊥面ACD;
(3)根据(2)可得AB⊥AD,由勾股定理和等积法,求出AO的长,即棱锥的高,进而可得三棱锥A-BCD的体积.
解答:
证明:(1)∵A在平面BCD上的投影O恰好在BD上.
∴AO⊥平面BCD,
又∵AO?平面ABD,
∴平面ABD⊥平面BCD,
又∵CD=6,BD=8,BC=10,
∴CD⊥BD,
又∵平面ABD∩平面BCD=BD,CD?平面BCD,
∴CD⊥平面ABD,
又∵AB?平面ABD,
∴AB⊥CD;
(2)∵AB=6,AC=8,BC=10,
∴AB⊥AC,
又∵AC∩CD=C,AC,CD?面ACD,
∴AB⊥面ACD;
(3)∵AD?面ACD;
∴AB⊥AD,
∴AD=
=2
,
∴AO=
=
,
故三棱锥A-BCD的体积V=
×
×6×8×
=12
∴AO⊥平面BCD,
又∵AO?平面ABD,
∴平面ABD⊥平面BCD,
又∵CD=6,BD=8,BC=10,
∴CD⊥BD,
又∵平面ABD∩平面BCD=BD,CD?平面BCD,
∴CD⊥平面ABD,
又∵AB?平面ABD,
∴AB⊥CD;

(2)∵AB=6,AC=8,BC=10,
∴AB⊥AC,
又∵AC∩CD=C,AC,CD?面ACD,
∴AB⊥面ACD;
(3)∵AD?面ACD;
∴AB⊥AD,
∴AD=
| BD2-AB2 |
| 7 |
∴AO=
| AB•AD |
| BD |
3
| ||
| 2 |
故三棱锥A-BCD的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
| 7 |
点评:本题考查的知识点是面面垂直的判定定理,面面垂直的性质定理,线面垂直的判定定理,线面垂直的性质定理,棱锥的体积,熟练掌握空间线线垂直,线面垂直与面面垂直的转化关系是解答的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
若集合A={x||x|≤1},B={x|
≤0},则A∩B为( )
| x-2 |
| x |
| A、[-1,0) |
| B、(0,1] |
| C、[0,2] |
| D、[0,1] |
命题“?x>0,x-lnx>0”的否定是( )
| A、?x>0,x-lnx≤0 |
| B、?x>0,x-lnx<0 |
| C、?x>0,x-lnx<0 |
| D、?x>0,x-lnx≤0 |
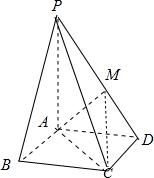 如图,四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,PA=2
如图,四棱锥P-ABCD的底面ABCD是矩形,侧棱PA⊥底面ABCD,PA=2