题目内容
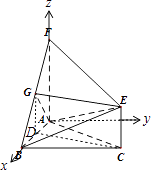
【题目】如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF 
2CE，G是线段BF上一点，AB=AF=BC． 
（Ⅰ）若EG∥平面ABC，求 
的值；
（Ⅱ）求二面角A﹣BF﹣E的大小的正弦值．
【答案】解：（Ⅰ）∵平面ABC⊥平面ACEF，且平面ABC∩平面ACEF=AC， AF⊥AC，∴AF⊥平面ABC，则平面ABF⊥平面ABC，
过G作GD⊥AB，垂足为D，则GD⊥平面ABC，连接CD，
由GD⊥平面ABC，AF⊥平面ABC，AF∥CE，可得GD∥CE，
又EG∥平面ABC，∴EG∥CD，则四边形GDCF为平行四边形，
∴GD=CE= 
，
∴ 
= 
；
（Ⅱ）由（Ⅰ）知AF⊥AB，AF⊥BC
∵BC⊥AB，∴BC⊥平面ABF．
如图，以A为原点，建立空间直角坐标系A﹣xyz．
则F（0，0，2），B（2，0，0），C（2，2，0），E（2，2，1），
=（0，2，0）是平面ABF的一个法向量．
设平面BEF的法向量 
=（x，y，z），则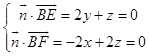
，令y=1，则z=﹣2，x=﹣2， =（﹣2，1，﹣2），
∴cos＜ ， ＞= 
= 
，
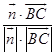∴二面角A﹣BF﹣E的正弦值为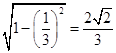 
．
【解析】（Ⅰ）由平面ABC⊥平面ACEF，且平面ABC∩平面ACEF=AC，可得AF⊥AC，则AF⊥平面ABC，得到平面ABF⊥平面ABC，过G作GD⊥AB，垂足为D，则GD⊥平面ABC，连接CD，可证得则四边形GDCF为平行四边形，从而得到GD=CE= 
，则G为BF的中点，得到 
的值；（Ⅱ）建立空间直角坐标系，利用向量法即可求二面角E﹣BF﹣A的余弦值．
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能正确解答此题．
