题目内容
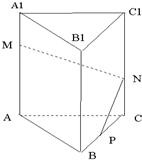 如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=6,M为AA1上的点,且AM=2MA1,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M点的最短路线长为4
如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=6,M为AA1上的点,且AM=2MA1,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M点的最短路线长为4| 2 |
(1)该三棱柱的侧面展开图的对角线长;
(2) PC和NC的长;
(3)此棱柱的表面积;
(4)平面NMP和平面ABC所成二面角(锐角)的大小(用反正切函数表示).
分析:(1)直接求解三棱柱的侧面展开图的对角线长;
(2)利用侧面展开图,MP1就是由点P沿棱侧面经过CC1到点M的最短路线.设PC=x,通过解三角形求出 PC和NC的长;
(3)直接求出底面面积,侧面面积即可得到此棱柱的表面积;
(4)连接PP1说明∠NHC所成二面就是平面NMP与平面ABC角的平面角,求出平面NMP和平面ABC所成二面角(锐角)的大小(用反正切函数表示).
(2)利用侧面展开图,MP1就是由点P沿棱侧面经过CC1到点M的最短路线.设PC=x,通过解三角形求出 PC和NC的长;
(3)直接求出底面面积,侧面面积即可得到此棱柱的表面积;
(4)连接PP1说明∠NHC所成二面就是平面NMP与平面ABC角的平面角,求出平面NMP和平面ABC所成二面角(锐角)的大小(用反正切函数表示).
解答:解:(1)正三棱柱ABC-A1B1C1的侧面展开图是一个长为9,宽为6的矩形,
其对角线长为
=
=3
;(3分)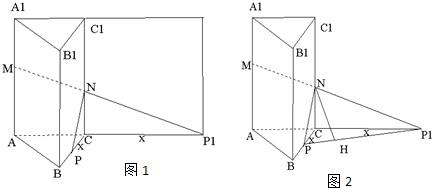
(2)如图1,将侧面BC1旋转120°使其与侧面AC1在同一平面上,点P运动到点P1的位置,连接MP1,则MP1就是由点P沿棱侧面经过CC1到点M的最短路线.设PC=x,
则P1C=x,在Rt△MAP1中,(3+x)2+42=32?x=1,
=
=
,∴NC=1(6分)
(3)棱柱的表面积为S表=S侧+2S底=6×9+2×
×32sin600=54+
.(8分)
(4)连接PP1(如图2),则PP1就是NMP与平面ABC的交线,作NH⊥PP1于H,又CC1⊥平面ABC,连接CH,由三垂线定理得,CH⊥PP1
∴∠NHC所成二面就是平面NMP与平面ABC角的平面角.(10分)
在Rt△PHC中,∵∠PCH=
∠PCP1=60°,
∴CH=
,在Rt△NCH中tan∠NHC=
=
,
即∠NHC=arctan
.(12分)
其对角线长为
| 92+62 |
| 117 |
| 13 |

(2)如图1,将侧面BC1旋转120°使其与侧面AC1在同一平面上,点P运动到点P1的位置,连接MP1,则MP1就是由点P沿棱侧面经过CC1到点M的最短路线.设PC=x,
则P1C=x,在Rt△MAP1中,(3+x)2+42=32?x=1,
| NC |
| MA |
| P1C |
| P1A |
| 1 |
| 4 |
(3)棱柱的表面积为S表=S侧+2S底=6×9+2×
| 1 |
| 2 |
9
| ||
| 2 |
(4)连接PP1(如图2),则PP1就是NMP与平面ABC的交线,作NH⊥PP1于H,又CC1⊥平面ABC,连接CH,由三垂线定理得,CH⊥PP1
∴∠NHC所成二面就是平面NMP与平面ABC角的平面角.(10分)
在Rt△PHC中,∵∠PCH=
| 1 |
| 2 |
∴CH=
| 1 |
| 2 |
| NC |
| CH |
| 2 |
| 3 |
即∠NHC=arctan
| 2 |
| 3 |
点评:本题考查转化思想的应用,空间几何问题常转化为平面几何问题解决,即空间问题平面化,要注意线线、线面、面面的平行、垂直关系的转化.求角与距离的关键是把距离与角转化为平面内的角与距离.
空间几何中的角有三类:1、两条异面直线所成的角:定义(略),范围:(00,900];
求法:平移--构成三角形,(一般是,见了中点找中点,形成中位线);2、直线与平面所成的角:
定义(略),范围:[00,900],求法:找射影--构成直角三角形.(一般是,作垂线,连垂足与斜足即射影,斜线,这三条线组成直角三角形);3、二面角:定义(略),范围:[00,1800],求法:找平面角,具体方法有四种:(1)定义法;(2)三垂线法;(3)垂面法;(4)射影面积法.
空间几何中的角有三类:1、两条异面直线所成的角:定义(略),范围:(00,900];
求法:平移--构成三角形,(一般是,见了中点找中点,形成中位线);2、直线与平面所成的角:
定义(略),范围:[00,900],求法:找射影--构成直角三角形.(一般是,作垂线,连垂足与斜足即射影,斜线,这三条线组成直角三角形);3、二面角:定义(略),范围:[00,1800],求法:找平面角,具体方法有四种:(1)定义法;(2)三垂线法;(3)垂面法;(4)射影面积法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上, (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.