题目内容
在△OAB中，
=
，
=
，OD是AB边上的高，若
=λ
，则实数λ等于（ ）
| OA |
| a |
| OB |
| b |
| AD |
| AB |
分析：根据向量的线性运算法则，算出
=
+λ(
-
)，再由OD⊥AB得
•
=0，由此建立关于
、
和λ的式子，解之即可得到实数λ的值．
| OD |
| a |
| b |
| a |
| OD |
| AD |
| a |
| b |
解答：解：∵
=λ
，
=
-
=
-
，
∴
=λ（
-
），可得
=
+
=
+λ(
-
)，
∵OD是AB边上的高，可得
⊥
，
∴
•
=0，即[
+λ(
-
)]•λ（
-
）=0，
解之得：λ=-
=
．
故选：A
| AD |
| AB |
| AB |
| OB |
| OA |
| b |
| a |
∴
| AD |
| b |
| a |
| OD |
| OA |
| AD |
| a |
| b |
| a |
∵OD是AB边上的高，可得
| OD |
| AD |
∴
| OD |
| AD |
| a |
| b |
| a |
| b |
| a |
解之得：λ=-
| ||||||
|
|
| ||||||
|
|
故选：A
点评：本题给出三角形的高，求边AC在AB边上的投影λ的值．着重考查了平面向量线性运算法则、向量数量积及其运算性质等知识，属于中档题．
练习册系列答案
相关题目
在△OAB中，
=
，
=
，M为OB的中点，N为AB的中点，ON，AM交于点P，则
=（ ）
| OA |
| a |
| OB |
| b |
| AP |
A、
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、-
|
如图所示，在△OAB中，OA＞OB，OC=OB，设
=
，
=
，若
=λ•
，则实数λ的值为（ ）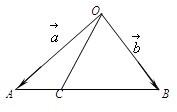
| OA |
| a |
| OB |
| b |
| AC |
| AB |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
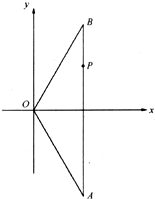（2006•广州一模）如下图，在△OAB中，|OA|=|OB|=4，点P分线段AB所成的比为3：1，以OA、OB所在直线为渐近线的双曲线M恰好经过点P，且离心率为2．