题目内容
5.设a>0,解不等式$\sqrt{{x}^{2}+1}$-ax≤1.分析 将不等式进行平方,讨论a的取值范围进行求解即可.
解答 解:由$\sqrt{{x}^{2}+1}$-ax≤1得$\sqrt{{x}^{2}+1}$≤ax+1,
即ax+1≥$\sqrt{{x}^{2}+1}$≥1,
则ax≥0,
∵a>0,
∴x≥0,
∴(ax+1)2≥x2+1,
即(a2-1)x2+2ax≥0,即x[(a2-1)x+2a]≥0.
当a=1时,上式变为2ax≥0,即x≥0,不等式的解集为{x|x≥0}.
当0<a<1 时,解得0≤x≤$\frac{2a}{1-{a}^{2}}$,不等式的解集为{x|0≤x≤$\frac{2a}{1-{a}^{2}}$}.
当a>1时,解得 x≤$\frac{2a}{1-{a}^{2}}$(舍)或x≥0,不等式的解集为{x|x≥0}
综上当a≥1时,不等式的解集为{x|x≥0}
当0<a<1时,不等式的解集为{x|0≤x≤$\frac{2a}{1-{a}^{2}}$}.
点评 本题主要考查根式不等式、一元二次不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
10.已知直线4x-3y+3=0与单位圆相交于点A、B,劣弧$\widehat{AB}$所对的圆心角为α,则sin(α+$\frac{π}{4}$)的值为( )
| A. | $\frac{7}{25}$ | B. | $\frac{7}{25}$$\sqrt{2}$ | C. | $\frac{17\sqrt{2}}{50}$ | D. | $\frac{17}{25}$$\sqrt{2}$ |
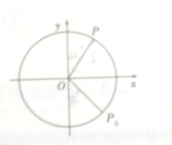 如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0($\sqrt{2}$,-$\sqrt{2}$),角速度为1,点P到x轴的距离d是关于时间t的函数,当t=$\frac{π}{4}$时,d=0.
如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0($\sqrt{2}$,-$\sqrt{2}$),角速度为1,点P到x轴的距离d是关于时间t的函数,当t=$\frac{π}{4}$时,d=0. 已知函数f(x)=x|x-2|,
已知函数f(x)=x|x-2|,