Question

16．如图甲，四边形ABCD中，E是BC的中点，DB=2，DC=1，BC=$\sqrt{5}$，AB=AD=$\sqrt{2}$．将（图甲）沿直线BD折起，使二面角A-BD-C为60°（如图乙），则点B到平面ACD的距为$\frac{2\sqrt{21}}{7}$．

Answer 1

分析 取BD中点M，连接AM，ME．先证明AM⊥BD，再证明BD⊥平面AEM，可得BD⊥AE，证明AE⊥ME，即可证明AE⊥平面BDC；建立空间直角坐标系，求得平面ACD的法向量，利用向量的距离公式，即可求得结论．

解答 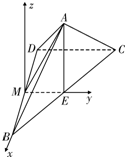解：如图，取BD中点M，连接AM，ME．
∵AB=AD=$\sqrt{2}$，∴AM⊥BD，
∵DB=2，DC=1，BC=$\sqrt{5}$，∴DB²+DC²=BC²，
∴△BCD是以BC为斜边的直角三角形，BD⊥DC，
∵E是BC的中点，∴ME为△BCD的中位线，∴ME∥$\frac{1}{2}$CD，
∴ME⊥BD，ME=$\frac{1}{2}$，
∴∠AME是二面角A-BD-C的平面角，∴∠AME=60°．
∵AM⊥BD，ME⊥BD且AM、ME是平面AME内两条相交于点M的直线，∴BD⊥平面AEM，
∵AE?平面AEM，∴BD⊥AE．
∵AB=AD=$\sqrt{2}$，DB=2，∴△ABD为等腰直角三角形，∴AM=$\frac{1}{2}$BD=1，
在△AME中，由余弦定理得：AE=$\frac{\sqrt{3}}{2}$，
∴AE²+ME²=1=AM²，∴AE⊥ME，
∵BD∩ME=M，BD?平面BDC，ME?平面BDC，∴AE⊥平面BDC
以M为原点，MB所在直线为x轴，ME所在直线为y轴，平行于EA的直线为z轴，建立空间直角坐标系，则B（1，0，0），E（0，$\frac{1}{2}$，0），A（0，$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），D（-1，0，0），C（-1，1，0）
则$\overrightarrow{AB}$=（1，-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$），$\overrightarrow{CD}$=（0，-1，0），$\overrightarrow{AD}$=（-1，-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$），
设平面ACD的法向量为$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{-x-\frac{1}{2}y-\frac{\sqrt{3}}{2}z=0}\\{-y=0}\end{array}\right.$
∴$\overrightarrow{n}$=（$\sqrt{3}$，0，-2），
记点B到平面ACD的距离为d，则d=|$\frac{\sqrt{3}+0+\sqrt{3}}{\sqrt{3+0+4}}$|=$\frac{2\sqrt{21}}{7}$．
故答案为：$\frac{2\sqrt{21}}{7}$．

点评 本题考查直线和平面垂直的证明，考查求点到平面的距离，考查向量知识的运用，属于中档题．