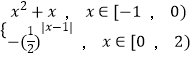题目内容
【题目】已知函数f（x）= 
+2x+sinx（x∈R），若函数y=f（x2+2）+f（﹣2x﹣m）只有一个零点，则函数g（x）=mx+ 
（x＞1）的最小值是 ．
【答案】5
【解析】解：∵函数f（x）= 
+2x+sinx满足﹣f（x）=﹣f（x），
且f′（x）=x2+2+cosx＞0恒成立，
故f（x）是R上的单调奇函数，
令y=f（x2+2）+f（﹣2x﹣m），
所以x2+2=2x+m，即x2﹣2x+2﹣m=0只有一个实数解，
则△=4﹣4（2﹣m）=0，解得m=1，
g（x）=x+ 
=x﹣1+ +1≥2 
+1=5
所以g（x）的最小值为5，
所以答案是：5．
【考点精析】根据题目的已知条件，利用函数的奇偶性和基本不等式的相关知识可以得到问题的答案，需要掌握偶函数的图象关于y轴对称；奇函数的图象关于原点对称；基本不等式：
,（当且仅当
时取到等号）；变形公式：
．
练习册系列答案
相关题目
