题目内容
【题目】定义域为R的函数f(x)满足f(x+3)=2f(x),当x∈[﹣1,2)时,f(x)= 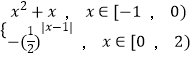 .
.
若存在x∈[﹣4,﹣1),使得不等式t2﹣3t≥4f(x)成立,则实数t的取值范围是 .
【答案】(﹣∞,1]∪[2,+∞)
【解析】解:当x∈[﹣1,2)时,f(x)= 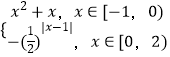 .
.
当x∈[﹣1,0)时,f(x)=(x+ ![]() )2﹣
)2﹣ ![]() ,仅有x=﹣
,仅有x=﹣ ![]() 时,取得最小值﹣
时,取得最小值﹣ ![]() ;
;
当x∈[0,2)时,f(x)=﹣( ![]() )|x﹣1|∈[﹣1,﹣
)|x﹣1|∈[﹣1,﹣ ![]() ],
],
可得x=1时,取得最小值﹣1;
则当x∈[﹣1,2)时,f(x)的最小值为﹣1.
当x∈[﹣4,﹣1),x+3∈[﹣1,2),
由f(x+3)=2f(x),可得
f(x)= ![]() f(x+3),由图象左右平移可知,函数的最值不变,
f(x+3),由图象左右平移可知,函数的最值不变,
可得此时f(x)的最小值为﹣ ![]() ,
,
由存在x∈[﹣4,﹣1),使得不等式t2﹣3t≥4f(x)成立,
可得t2﹣3t≥4f(x)的最小值,即为t2﹣3t≥﹣2,
解得t≥2或t≤1,
所以答案是:(﹣∞,1]∪[2,+∞).

练习册系列答案
相关题目