题目内容
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.(Ⅰ)证明EF∥平面PAB;
(Ⅱ)证明EF⊥平面PBC;
(III)点M是四边形ABCD内的一动点,PM与平面ABCD所成的角始终为45°,求动直线PM所形成的曲面与平面ABCD、平面PAB、平面PAD所围成几何体的体积.

【答案】分析:(I)线段PB的中点为G,连接EG,AG,由三角形的中位线定理,平行四边形的判定与性质,我们易得到EF∥AG,结合线面平行的判定定理,我们易得到EF∥平面PAB;
(II)根据已知中PA⊥平面ABCD,PA=AB=2,及PA=PB,G为AB的中点,结合线面垂直的性质及等腰三角形三线合一,我们易证明AG⊥平面PBC,结合(I)中结论EF∥AG,即可得到结论;
(III)根据点M是四边形ABCD内的一动点,PM与平面ABCD所成的角始终为45°,我们根据旋转体的定义判断出动直线PM所形成的曲面与平面ABCD、平面PAB、平面PAD所围成几何体的形状及底面半径、高等几何量,代入圆锥体积公式,即可得到答案.
解答:证明:(I)设线段PB的中点为G,连接EG,AG,
∵E为PC的中点,
∴EG∥BC且EG= BC
BC
又∵F为AD的中点,四边形ABCD为正方形
∴AF∥BC且AF= BC
BC
∴EG∥AF且EG=AF
∴四边形EGAF为平行四边形
∴EF∥AG
又∵EF?平面PAB,AG?平面PAB
∴EF∥平面PAB;
(II)∵PA⊥平面ABCD,BC?平面ABCD,
∴BC⊥PA,
又∵BC⊥AB,AB?平面PAB,AP?平面PAB,AP∩AB=A
∴BC⊥平面PAB
又∵AG?平面PAB
∴AG⊥BC
又∵PA=PB,G为AB的中点
∴AG⊥PB
又∵PB?平面PBC,BC?平面PBC,PB∩BC=B
∴AG⊥平面PBC,
由(I)知EF∥AG
∴EF⊥平面PBC;
解:(III)∵PM与平面ABCD所成的角始终为45°,PA⊥平面ABCD,
∴AM=PA=2,
又∵∠BAD=90°
∴点M的是以A为圆心,2为半径的四分之一圆,
∴动直线PM所形成的曲面与平面ABCD、平面PAD围志的几何是底面半径为2,高为2的四分之一圆锥
∴V= =
=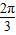
点评:本题考查的知识点是直线与平面垂直的判定,圆锥的体积及直线与平面平行的判定,其中熟练掌握空间中线与面垂直及平行的判定和性质,建立良好的空间能力是解答此类问题的关键.
(II)根据已知中PA⊥平面ABCD,PA=AB=2,及PA=PB,G为AB的中点,结合线面垂直的性质及等腰三角形三线合一,我们易证明AG⊥平面PBC,结合(I)中结论EF∥AG,即可得到结论;
(III)根据点M是四边形ABCD内的一动点,PM与平面ABCD所成的角始终为45°,我们根据旋转体的定义判断出动直线PM所形成的曲面与平面ABCD、平面PAB、平面PAD所围成几何体的形状及底面半径、高等几何量,代入圆锥体积公式,即可得到答案.
解答:证明:(I)设线段PB的中点为G,连接EG,AG,
∵E为PC的中点,
∴EG∥BC且EG=
 BC
BC又∵F为AD的中点,四边形ABCD为正方形
∴AF∥BC且AF=
 BC
BC∴EG∥AF且EG=AF
∴四边形EGAF为平行四边形
∴EF∥AG
又∵EF?平面PAB,AG?平面PAB
∴EF∥平面PAB;
(II)∵PA⊥平面ABCD,BC?平面ABCD,
∴BC⊥PA,
又∵BC⊥AB,AB?平面PAB,AP?平面PAB,AP∩AB=A
∴BC⊥平面PAB
又∵AG?平面PAB
∴AG⊥BC
又∵PA=PB,G为AB的中点
∴AG⊥PB
又∵PB?平面PBC,BC?平面PBC,PB∩BC=B
∴AG⊥平面PBC,
由(I)知EF∥AG
∴EF⊥平面PBC;
解:(III)∵PM与平面ABCD所成的角始终为45°,PA⊥平面ABCD,
∴AM=PA=2,
又∵∠BAD=90°
∴点M的是以A为圆心,2为半径的四分之一圆,
∴动直线PM所形成的曲面与平面ABCD、平面PAD围志的几何是底面半径为2,高为2的四分之一圆锥
∴V=
 =
=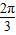
点评:本题考查的知识点是直线与平面垂直的判定,圆锥的体积及直线与平面平行的判定,其中熟练掌握空间中线与面垂直及平行的判定和性质,建立良好的空间能力是解答此类问题的关键.

练习册系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,