题目内容
12.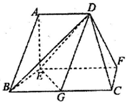 在如图所示的多面体中,底面BCFE是梯形,EF∥BC,EF⊥EB,平面ABE与平面BCFE所成的角为直二面角,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$,G为BC中点.
在如图所示的多面体中,底面BCFE是梯形,EF∥BC,EF⊥EB,平面ABE与平面BCFE所成的角为直二面角,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$,G为BC中点.(Ⅰ)求证:AE⊥平面BCFE;
(Ⅱ)求异面直线AE与CD所成角的正切;
(Ⅲ)求证:BD⊥EG.
分析 (Ⅰ)由面面垂直的性质得EF⊥平面ABE,由勾股定理得AE⊥BE,由此能证明AE⊥面BCFE.
(Ⅱ)由垂直得AE⊥EG,从而得到AG∥CD,进而得到∠EAG是异面直线AE与CD所成的角,由此能求出异面直线AE与CD所成的角的正切值
(Ⅲ)过D作DH∥AE,交EF于H,由线面垂直得DH⊥GE,从而GE⊥平面BDH,由此能证明GE⊥BD.
解答 (Ⅰ)证明:∵平面ABE⊥平面BCFE,交线为BE,EF⊥BE,
∴EF⊥平面ABE,
∵AE=BE=2,AB=2$\sqrt{2}$,∴AE2+BE2=AB2,∴AE⊥BE,
又∵BE∩EF=E,∴AE⊥面BCFE.
(Ⅱ)解:由(Ⅰ)得AE⊥平面BCFE,
∵EG?平面BCFE,∴AE⊥EG,
又由已知得AD$\underset{∥}{=}$GC,连结AG,得平行四边形ADCG,
∴AG∥CD,
∵∠EAG为锐角,∴∠EAG是异面直线AE与CD所成的角,
又∵BE=BG=2,∠EBG=90°,∴EG=2$\sqrt{2}$,∴tan$∠EAG=\sqrt{2}$,
∴异面直线AE与CD所成的角的正切值为$\sqrt{2}$.
(Ⅲ)证明:过D作DH∥AE,交EF于H,连结GH,BH,
∵AE⊥平面BCFE,∴DH⊥面BCFE,
∴DH⊥GE,
由(Ⅰ)(Ⅱ)知,四边形BGHE为正方形,∴BH⊥GE,
又∵BH∩DH=H,∴GE⊥平面BDH,
∴GE⊥BD.
点评 本题考查线面垂直的证明,考查异面直线所成角的正切值的求法,考查线线垂直的证明,是中档题,解题时要注意空间中线线、线面、面面间的位置关系和性质的合理运用.

练习册系列答案
相关题目
4.若x,y是非负整数,那么满足方程25+y2=x2的解有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
2.如果y是x的函数,x=$\sqrt{t+1}$,y=$\sqrt{t-1}$,其中t>1,则y与x的函数表达式为( )
| A. | y=$\sqrt{{x}^{2}-2}$ (x>2) | B. | y=$\sqrt{x-2}$(x>2) | C. | y=$\sqrt{{x}^{2}-2}$ (x>$\sqrt{2}$) | D. | y=$\sqrt{x-2}$(x>$\sqrt{2}$) |
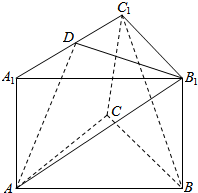 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.