题目内容
3.已知向量$\overrightarrow{m}$=(3,4),|$\overrightarrow{m}$-$\overrightarrow{n}$|=1,则|$\overrightarrow{n}$|的取值范围是[4,6].分析 由题意可得|$\overrightarrow{m}$|=5、|$\overrightarrow{m}$-$\overrightarrow{n}$|=1,再利用绝对值三角不等式求得|$\overrightarrow{n}$|的取值范围.
解答 解:由题意可得|$\overrightarrow{m}$|=5,再根据|$\overrightarrow{m}$-$\overrightarrow{n}$|=1,-|$\overrightarrow{m}$|+|$\overrightarrow{n}$|≤|$\overrightarrow{m}$-$\overrightarrow{n}$|≤|$\overrightarrow{m}$|+|$\overrightarrow{n}$|,
可得|$\overrightarrow{n}$|-5≤1≤5+|$\overrightarrow{n}$|,且5-|$\overrightarrow{n}$|≤1≤5+|$\overrightarrow{n}$|求得4≤|$\overrightarrow{n}$|≤6,
故答案为:[4,6].
点评 本题主要考查绝对值三角不等式,求向量的模,属于基础题.

练习册系列答案
相关题目
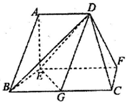 在如图所示的多面体中,底面BCFE是梯形,EF∥BC,EF⊥EB,平面ABE与平面BCFE所成的角为直二面角,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$,G为BC中点.
在如图所示的多面体中,底面BCFE是梯形,EF∥BC,EF⊥EB,平面ABE与平面BCFE所成的角为直二面角,AD∥EF,BC=2AD=4,EF=3,AE=BE=2,AB=2$\sqrt{2}$,G为BC中点.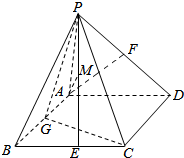 已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点
已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点