题目内容

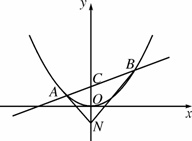在平面直角坐标系xOy中，过定点C(0，p)作直线与抛物线x2=2px(p>0)相交于A、B两点.

（Ⅰ）若点N是点C关于坐标原点O的对称点，

求△ANB面积的最小值；

（Ⅱ）是否存在垂直于y轴的直线l，使得l被以AC为直径的圆截得弦长恒为定值？若存在，求出l的方程；若不存在，说明理由.（此题不要求在答题卡上画图）

本小题主要考查直线、圆和抛物线等平面解析几何的基础知识，考查综合运用数学知识进行推理运算的能力和解决问题的能力.

（Ⅰ）依题意，点N的坐标为N(0,-p),可设A(x1,y1),B(x2,y2)，直线AB的方程为y=kx+p,与x2=2py联立得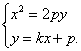消去y得x2-2pkx-2p2=0.

由韦达定理得x1+x2=2pk,x1x2=-2p2.

于是

　　　　　＝

　　　　　＝

.

(Ⅱ)假设满足条件的直线l存在，其方程为y=a,AC的中点为径的圆相交于点P、Q，PQ的中点为H，则

＝.

=

＝

        =

令，得为定值，故满足条件的直线l存在，其方程为，

即抛物线的通径所在的直线

练习册系列答案
相关题目
在平面直角坐标系xoy中，已知圆心在直线y=x+4上，半径为2
2
的圆C经过坐标原点O，椭圆
x2
a2
+
y2
9
=1(a＞0)与圆C的一个交点到椭圆两焦点的距离之和为10．
（1）求圆C的方程；
（2）若F为椭圆的右焦点，点P在圆C上，且满足PF=4，求点P的坐标．
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是
3
5
，点B的纵坐标是
12
13
，则sin（α+β）的值是
16
65
16
65
．
在平面直角坐标系xOy中，若焦点在x轴的椭圆
x2
m
+
y2
3
=1的离心率为
1
2
，则m的值为
4
4
．
（2013•泰州三模）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知A（0，1），B（0，-1），C（t，0），D(
3t
，0)，其中t≠0．设直线AC与BD的交点为P，求动点P的轨迹的参数方程（以t为参数）及普通方程．
（2013•东莞一模）在平面直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左焦点为F1（-1，0），且椭圆C的离心率e=
1
2
．
（1）求椭圆C的方程；
（2）设椭圆C的上下顶点分别为A1，A2，Q是椭圆C上异于A1，A2的任一点，直线QA1，QA2分别交x轴于点S，T，证明：|OS|•|OT|为定值，并求出该定值；
（3）在椭圆C上，是否存在点M（m，n），使得直线l：mx+ny=2与圆O：x2+y2=
16
7
相交于不同的两点A、B，且△OAB的面积最大？若存在，求出点M的坐标及对应的△OAB的面积；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网