题目内容
下列四边形中，四个顶点一定在同一个圆上的是（ ）
| A、平行四边行 | B、菱形 | C、矩形 | D、直角梯形 |
考点：圆內接多边形的性质与判定
专题：选作题,几何证明
分析：四个顶点可在同一个圆上的四边形，一定有一点到它的四个顶点的距离都相等，因而A、B、D都是错误的；矩形的四个顶点到对角线的交点的距离都相同，因而矩形的四个顶点一定可以在同一个圆上；
解答：解：∵矩形对角线相等且互相平分，
∴四个顶点到对角线交点距离相等，
∴矩形四个顶点定可在同一个圆上．
故选：C．
∴四个顶点到对角线交点距离相等，
∴矩形四个顶点定可在同一个圆上．
故选：C．
点评：此题主要考查的是圆内接四边形的性质，理解四个顶点在同一个圆上的条件是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
调查某医院某段时间内婴儿出生的时间与性别的关系，得到下面的数据表：
你认为婴儿的性别与出生时间有关系的把握为（ ）
| 晚上 | 白天 | 合计 | |
| 男婴 | 24 | 30 | 54 |
| 女婴 | 8 | 26 | 34 |
| 合计 | 32 | 56 | 88 |
| A、80% | B、90% |
| C、95% | D、99% |
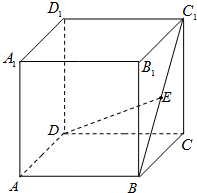如图，在正方体ABCD-A1B1C1D1中，E为BC1的中点，则DE与面BCC1B1所成角的正切值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使△ABE和△ACD相似的是（ ）| A、∠B=∠C | B、∠ADC=∠AEB | C、BE=CD，AB=AC | D、AD：AC=AE：AB |
已知，在Rt△ABC中，CD为斜边上的高，CE平分∠BCD，交AB于点E．求证：AE2=AD•AB．
如图，AB是圆O的直径，C，D是圆O上两点，AC与BD相交于点E，GC，GD是圆O的切线，点F在DG的延长线上，且DG=GF．求证：矩阵A=
，向量
=
，则A10
=（ ）
|
| α |
|
| α |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
在极坐标系中，点F（1，0）到直线θ=
（ρ∈R）的距离是（ ）
| π |
| 4 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
，
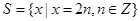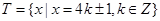则 （ ）
