题目内容
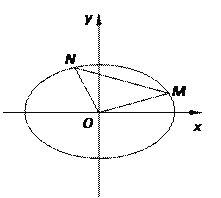
【题目】已知焦距为2的椭圆W: ![]() (a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为
(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为![]() .
.
(1)求椭圆W的标准方程;
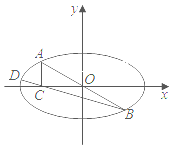
(2)如图所示,点A,D是椭圆W上两点,点A与点B关于原点对称,AD⊥AB,点C在x轴上,且AC与x轴垂直,求证:B,C,D三点共线.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据椭圆的定义和性质,建立方程求出a,b即可.
(2)联立直线和椭圆方程,利用消元法结合设而不求的思想进行求解即可.
试题解析:
(1)由题意可知:2c=2,c=1,a2-b2=1,
∵M(x0,y0)为椭圆W上不在坐标轴上的任意一点,
∴![]() ,
,![]() =
=![]() (a2-
(a2-![]() ),
),![]() =
=![]() (b2-
(b2-![]() ),
),
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]() =
=![]()
![]() ,
,
=![]()
![]() =(
=(![]() )2=
)2=![]() ,则a2=2b2,
,则a2=2b2,
∴a2=2,b2=1,
∴椭圆W的标准方程![]() ;
;
(2)证明:不妨设点A(x1,
∵A,D在椭圆上,![]() ,=0,即(x1-x2)(x1+x2)+2(y1-y2)(y1+y2)=0,
,=0,即(x1-x2)(x1+x2)+2(y1-y2)(y1+y2)=0,
∴![]() =-
=-![]() ,
,
由AD⊥AB,
∴kADkAB=-1,![]()
![]() =-1,
=-1,![]() (-
(-![]() ,)=-1,
,)=-1,
∴![]() =
=![]() ,
,
∴kBD-kBC=![]() -
-![]() =
=![]() -
-![]() =0,
=0,
kBD=kBC,
∴B,C,D三点共线.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目