题目内容
4.函数f(x)=$\frac{x-3}{\sqrt{x-4}}$的定义域为(4,+∞),值域为[2,+∞).分析 定义域容易看出为(4,+∞),可将原函数变成$f(x)=\sqrt{x-4}+\frac{1}{\sqrt{x-4}}$,根据基本不等式即可得出f(x)≥2,即得出f(x)的值域.
解答 解:要使f(x)有意义,则x>4;
∴该函数定义域为(4,+∞);
$f(x)=\frac{x-4+1}{\sqrt{x-4}}=\sqrt{x-4}+\frac{1}{\sqrt{x-4}}$≥2,当$\sqrt{x-4}=\frac{1}{\sqrt{x-4}}$,即x=5时取“=”;
∴该函数的值域为[2,+∞).
故答案为:(4,+∞),[2,+∞).
点评 考查函数定义域、值域的概念及求法,基本不等式用于求函数值域,注意判断等号能否取到.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
15.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且当x∈[-1,0)时f(x)=($\frac{1}{2}$)x,则 f(log28)等于( )
| A. | 3 | B. | $\frac{1}{8}$ | C. | -2 | D. | 2 |
12.填表:
| 角α | 0° | 90° | 180° | 270° | 360° |
| α的弧度数 | |||||
| sinα | |||||
| cosα | |||||
| tanα |
 三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)
三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小) 中,
中,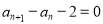 ,且
,且 ,则
,则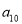 等于( )
等于( )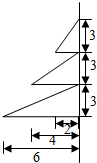 三个直角三角形如图放置,它们围绕固定直线旋转一周形成几何体,画出它的三视图,并求出它的表面积和体积.
三个直角三角形如图放置,它们围绕固定直线旋转一周形成几何体,画出它的三视图,并求出它的表面积和体积.