题目内容
6．Rt△ABC中．|AB|=2a（a＞0），求直角顶点C的轨迹方程．分析 以AB为x轴，中垂线为y轴建立坐标系，设直角顶点C（x，y），则利用|OC|=$\frac{1}{2}$|AB|，可得直角顶点C的轨迹方程．
解答 解：以AB为x轴，中垂线为y轴建立坐标系，则A（-a，0），B（a，0），
设直角顶点C（x，y），则利用|OC|=$\frac{1}{2}$|AB|，
可得直角顶点C的轨迹方程x2+y2=a2（x≠±a）．
点评 本题考查直角顶点C的轨迹方程，考查学生的计算能力，是基础题．
练习册系列答案
蓝天教育暑假优化学习系列答案
相关题目
16．下列各函数中，图象完全相同的是（ ）
| A． | y=2lgx和y=lgx2 | B． | y=$\frac{|x-1|}{x-1}$和y=$\left\{\begin{array}{l}{-1，x∈（-∞，1）}\\{1，x∈（1，+∞）}\end{array}\right.$ | ||
| C． | y=$\frac{{x}^{2}}{x}$和y=x | D． | y=x-3和y=$\sqrt{（x-3）^{2}}$ |
1．将-$\frac{25}{6}$π化成a+2kπ（k∈Z，0≤a＜2π）的形式为（ ）
| A． | -$\frac{25}{6}$π=-5π+$\frac{5}{6}$π | B． | -$\frac{25}{6}$π=-6π+$\frac{11}{6}$π | C． | -$\frac{25}{6}$π=-4π-$\frac{π}{6}$ | D． | -$\frac{25}{6}$π=-3π-$\frac{7}{6}$π |
11．函数y=log2x+log22（2x2）的值域是（ ）
| A． | （-∞，0] | B． | [4，+∞） | C． | [0，4] | D． | [-$\frac{9}{16}$，+∞） |
15．
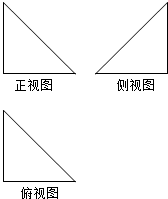若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形，则这个空间几何体的外接球的表面积和内切球的表面积之比是（ ）
若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形，则这个空间几何体的外接球的表面积和内切球的表面积之比是（ ）| A． | $\frac{18+9\sqrt{3}}{2}$ | B． | 18+9$\sqrt{3}$ | C． | 3 | D． | 9 |
17．下列各函数中，最小值为2的是（ ）
| A． | y=x+$\frac{1}{x}$ | B． | y=sinx+$\frac{1}{sinx}$，x∈（0，$\frac{π}{2}$） | ||
| C． | y=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$ | D． | $y=x+\frac{1}{4（x-2）}-1（x＞2）$ |