题目内容
已知f(1,1)=1,f(m,n)∈N*(m,n∈N*),且对任意的m,n∈N*都有:
(1)f(m,n+1)=f(m,n)+2.
(2)f(m+1,1)=2f(m,1).
给出以下三个结论:①f(1,5)=9;②f(5,1)=16;
③f(5,6)=26.其中正确结论的序号有 .
(1)f(m,n+1)=f(m,n)+2.
(2)f(m+1,1)=2f(m,1).
给出以下三个结论:①f(1,5)=9;②f(5,1)=16;
③f(5,6)=26.其中正确结论的序号有 .
①②③
在(1)式中令m=1可得
f(1,n+1)=f(1,n)+2,
则f(1,5)=f(1,4)+2=…=9;
在(2)式中,由f(m+1,1)=2f(m,1)得,
f(5,1)=2f(4,1)=…=16f(1,1)=16,
从而f(5,6)=f(5,1)+10=26,故①②③均正确.
f(1,n+1)=f(1,n)+2,
则f(1,5)=f(1,4)+2=…=9;
在(2)式中,由f(m+1,1)=2f(m,1)得,
f(5,1)=2f(4,1)=…=16f(1,1)=16,
从而f(5,6)=f(5,1)+10=26,故①②③均正确.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 .将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,则类比的结论为
.将这个结论类比到空间:在三棱锥A-BCD中,平面DEC平分二面角A-CD-B且与AB交于E,则类比的结论为 =________.
=________.
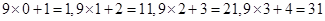 ,……,猜想第
,……,猜想第 (
(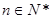 )个等式应为_ _.
)个等式应为_ _. 通过观察上述不等式的规律,则关于正数
通过观察上述不等式的规律,则关于正数 满足的不等式是
满足的不等式是 .
. 结论
结论