题目内容
10.设P,Q分别为直线x-y=0和圆x2+(y-6)2=2上的点,则|PQ|的最小值为( )| A. | $2\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $4\sqrt{2}$ | D. | 4 |
分析 先由条件求得圆心(0,6)到直线x-y=0的距离为d的值,则d减去半径,即为所求.
解答 解:由题意可得圆心(0,6)到直线x-y=0的距离为d=$\frac{|0-6|}{\sqrt{2}}$=3$\sqrt{2}$,圆的半径r=$\sqrt{2}$,
故|PQ|的最小值为d-r=2$\sqrt{2}$,
故选:A.
点评 本题主要考查圆的标准方程,直线和圆的位置关系,点到直线的距离公式的应用,属于基础题.

练习册系列答案
相关题目
20.已知i为虚数单位,复数z=a+bi(a,b∈R)的虚部b记作Im(z),则Im($\frac{1}{1+i}$)=( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
1.如图复平面内的点A表示复数z,则复数$\frac{z}{1+i}$表示的点所在的象限为( )
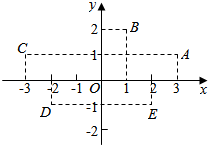
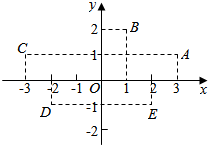
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.向量$\overrightarrow{a}$与$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,且$\overrightarrow{a}⊥\overrightarrow{b}$,则|$\overrightarrow{a}+\overrightarrow{b}$|为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$ |
5.已知a,b∈R,则命题“若a2+b2=0,则a=0或b=0”的否命题是( )
| A. | 若a2+b2≠0,则a≠0且b≠0 | B. | 若a2+b2≠0,则a≠0或b≠0 | ||
| C. | 若a≠0且b≠0,则a2+b2≠0 | D. | 若a≠0或b≠0,则a2+b2≠0 |
19.已知x,y满足$\left\{\begin{array}{l}{kx-y+2≥0(k<0)}\\{x+y-2≥0}\\{y≥0}\end{array}\right.$,则使目标函数z=y-x取得最小值-4的最优解为( )
| A. | (2,-2) | B. | (-4,0) | C. | (4,0) | D. | (7,3) |
20.已知集合A={x|x(x-3)<0},B={x||x-1|<2},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |