题目内容
20.如图,椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,F为右焦点,过F作直线l交椭圆于C、D两点,求△OCD面积的最大值.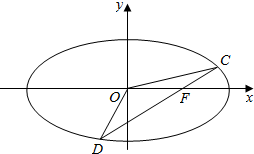
分析 通过设直线l方程为x=my+$\sqrt{2}$,并与椭圆方程联立,利用韦达定理可知yC+yD=-$\frac{2\sqrt{2}m}{{m}^{2}+2}$、yCyD=-$\frac{2}{{m}^{2}+2}$,通过完全平方公式可知|yC-yD|=$\frac{4}{{m}^{2}+2}$•$\sqrt{{m}^{2}+1}$,通过换元法及基本不等式可知|yC-yD|≥2,利用S△OCD=S△OCF+S△ODF计算即得结论.
解答 解:依题意,F($\sqrt{2}$,0),OF=$\sqrt{2}$,
设直线l方程为:x=my+$\sqrt{2}$,并与椭圆方程联立,
消去y、整理得:(m2+2)y2+$2\sqrt{2}$my-2=0,
∴yC+yD=-$\frac{2\sqrt{2}m}{{m}^{2}+2}$,yCyD=-$\frac{2}{{m}^{2}+2}$,
∴|yC-yD|=$\sqrt{({y}_{C}+{y}_{D})^{2}-4{y}_{C}{y}_{D}}$
=$\sqrt{(-\frac{2\sqrt{2}m}{{m}^{2}+2})^{2}+\frac{8}{{m}^{2}+2}}$
=$\frac{4}{{m}^{2}+2}$•$\sqrt{{m}^{2}+1}$,
记t=$\sqrt{{m}^{2}+1}$,则m2=t2-1,
∴|yC-yD|=$\frac{4t}{{t}^{2}+1}$=$\frac{4}{t+\frac{1}{t}}$≤$\frac{4}{2\sqrt{t•\frac{1}{t}}}$=2(当且仅当$t=\frac{1}{t}$即t=1时等号成立),
∴当t=1即m=0时,|yC-yD|取最大值2,
∴S△OCD=S△OCF+S△ODF
=$\frac{1}{2}$OF•|yC|+$\frac{1}{2}$OF•|yD|
=$\frac{1}{2}$OF•|yC-yD|
=$\frac{\sqrt{2}}{2}$•|yC-yD|
≥$\frac{\sqrt{2}}{2}•2$
=$\sqrt{2}$,
∴△OCD面积的最大值为$\sqrt{2}$.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于中档题.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | {0}是空集 | B. | {x∈Q|$\frac{6}{x}$∈N}是有限集 | ||
| C. | {x∈Q|x2+x+2=0}是空集 | D. | {1,2}和{2,1}是不同的集合 |