题目内容
【题目】已知椭圆![]() (a>b>0)过点(0,
(a>b>0)过点(0,![]() ),且离心率为
),且离心率为![]() 。
。
(Ⅰ)求椭圆E的方程;
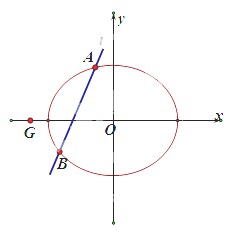
(II)设直线x my 1,(m R)交椭圆E与A,B两点,判断点G(-![]() ,0)与以线段AB为直径的圆的位置关系,并说明理由。
,0)与以线段AB为直径的圆的位置关系,并说明理由。
【答案】(Ⅰ)![]() ;(Ⅱ)G(-
;(Ⅱ)G(-![]() ,0)在以AB为直径的圆外。
,0)在以AB为直径的圆外。
【解析】解法一:(I)由已知得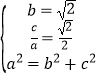 ,解得
,解得 所以椭圆E得方程为
所以椭圆E得方程为![]() 。
。
(II)设点![]() ,
,![]() ,AB中点为
,AB中点为![]() 由
由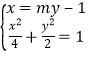 得
得![]() ,
,
所以![]() ;
;![]() ,从而
,从而![]()
所以![]() .
.![]()
![]()
故![]()
![]()
所以![]() ,故
,故![]() 在以AB为直径的圆外。
在以AB为直径的圆外。
解答二:(I)同解法一
(II)设点![]() ,
,![]() ,则
,则![]()
由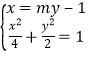 得
得![]() ,所以
,所以![]() ;
;![]() ,
,
从而![]()
![]()
![]()
所以![]() ,又
,又![]() 不共线,所以
不共线,所以![]() 为锐角。
为锐角。
故点![]() 在以AB为直径的圆外。
在以AB为直径的圆外。
【考点精析】认真审题,首先需要了解点与圆的位置关系(点![]() 与圆
与圆![]() 的位置关系有三种:若
的位置关系有三种:若![]() ,则
,则![]() 点
点![]() 在圆外;
在圆外;![]() 点
点![]() 在圆上;
在圆上;![]() 点
点![]() 在圆内),还要掌握椭圆的标准方程(椭圆标准方程焦点在x轴:
在圆内),还要掌握椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
