题目内容
(本题满分14分)设有关于 的一元二次方程
的一元二次方程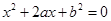 .
.
(1)若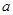 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,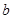 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若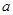 是从区间[0,3]任取的一个数,
是从区间[0,3]任取的一个数,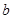 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.
(1)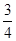 (2)
(2)
解析试题分析:记事件 为“方程
为“方程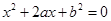 有实根”,
有实根”,
当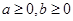 时,方程
时,方程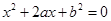 有实根的充要条件为
有实根的充要条件为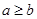 .
.
(1)基本事件共有12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),其中第一个数表示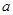 的取值,第二个数表示
的取值,第二个数表示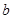 的取值.
的取值.
事件 中包含9个基本事件,事件
中包含9个基本事件,事件 发生的概率为
发生的概率为
P( )=
)=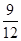 =
=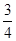 . ……7分
. ……7分
(2)试验的全部结果所构成的区域为
{(a,b)|0≤a≤3,0≤b≤2}.
构成事件 的区域为
的区域为
{(a,b)|0≤a≤3,0≤b≤2,a≥b},
所以所求的概率为 =
=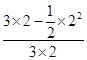 =
= . ……14分
. ……14分
考点:本小题主要考查古典概型和几何概型的概率求解公式的应用,考查学生的分析问题、解决问题的能力和运算求解能力和分类讨论思想和划归思想的应用.
点评:要高考中古典概型和几何概型在选择题、填空题和与其他知识点相结合的解答题中均有考查. 解决此类问题,应掌握计算古典概型、几何概型的常用方法.

(本小题满分12分)
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为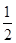 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
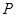 | 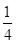 |  | 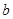 | 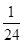 |
(2) 求
 ,
, 的值;
的值;(3) 求
 的数学期望.
的数学期望. 公安部发布酒后驾驶处罚的新规定(一次性扣罚12分)已于2011年4月1日起正式施行.酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量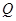 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当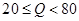 时,为酒后驾车;当
时,为酒后驾车;当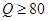 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
依据上述材料回答下列问题:
(Ⅰ)分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率;
(Ⅱ)从酒后违法驾车的司机中,抽取2人,请一一列举出所有的抽取结果,并求取到的2人中含有醉酒驾车的概率. (酒后驾车的人用大写字母如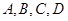 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如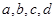 表示)
表示)
| 血酒含量 | (0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120] |
| 人数 | 194 | 1 | 2 | 1 | 1 | 1 |
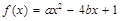 .
. 在区间
在区间 上是增函数的概率;
上是增函数的概率; 内的一点,求函数
内的一点,求函数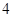 名男生和
名男生和 名女生中任选
名女生中任选 人参加演讲比赛,
人参加演讲比赛, 名女生的概率;③求所选
名女生的概率;③求所选