题目内容
给出定义:若m-| 1 |
| 2 |
| 1 |
| 2 |
①函数y=f(x)的定义域为R,值域为[0,
| 1 |
| 2 |
②函数y=f(x)的图象关于直线x=
| k |
| 2 |
③函数y=f(x)是周期函数,最小正周期为1;
④函数y=f(x)在[-
| 1 |
| 2 |
| 1 |
| 2 |
其中正确的命题的序号
分析:本题为新定义问题,因为m为整数,故可取m为几个特殊的整数进行研究.
解答: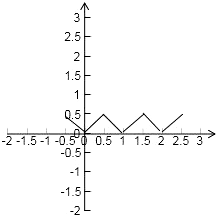 解:由题意x-{x}=x-m,f(x)=|x-{x}|=|x-m|,
解:由题意x-{x}=x-m,f(x)=|x-{x}|=|x-m|,
m=0时,-
<x≤
,f(x)=|x|,
m=1时,1-
<x≤1+
,f(x)=|x-1|,
m=2时,2-
<x≤2+
,f(x)=|x-2|,
由图象可知正确命题为①②③,
故答案为:①②③.
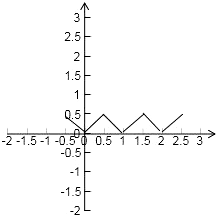 解:由题意x-{x}=x-m,f(x)=|x-{x}|=|x-m|,
解:由题意x-{x}=x-m,f(x)=|x-{x}|=|x-m|,m=0时,-
| 1 |
| 2 |
| 1 |
| 2 |
m=1时,1-
| 1 |
| 2 |
| 1 |
| 2 |
m=2时,2-
| 1 |
| 2 |
| 1 |
| 2 |
由图象可知正确命题为①②③,
故答案为:①②③.
点评:本题是新定义问题,考查函数的性质,可结合图象进行研究,体现数形结合思想.

练习册系列答案
相关题目