题目内容
(本题满分12分) 已知函数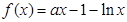
 .
.
(1)讨论函数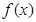 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数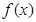 在
在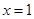 处取得极值,对
处取得极值,对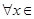
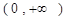 ,
,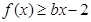 恒成立,求实数
恒成立,求实数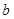 的取值范围;
的取值范围;
(3)当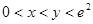 且
且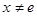 时,试比较
时,试比较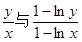 的大小.
的大小.
(1)当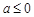 时
时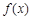 在
在 上没有极值点,
上没有极值点,
当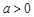 时,
时,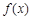 在
在 上有一个极值点(2)
上有一个极值点(2)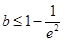 (3)当0<x<e时
(3)当0<x<e时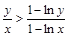 ,当e<x<e2时
,当e<x<e2时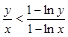
解析试题分析:(Ⅰ)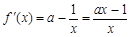 ,当
,当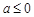 时,
时,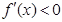 在
在 上恒成立,函数
上恒成立,函数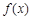 在
在 单调递减,∴
单调递减,∴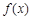 在
在 上没有极值点;
上没有极值点;
当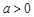 时,
时,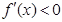 得
得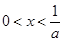 ,
,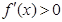 得
得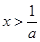 ,
,
∴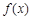 在
在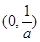 上递减,在
上递减,在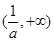 上递增,即
上递增,即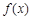 在
在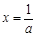 处有极小值.
处有极小值.
∴当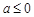 时
时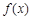 在
在 上没有极值点,
上没有极值点,
当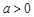 时,
时,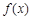 在
在 上有一个极值点.-----3分
上有一个极值点.-----3分
(Ⅱ)∵函数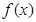 在
在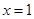 处取得极值,∴
处取得极值,∴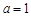 ,
,
∴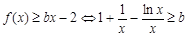 ,---------5分
,---------5分
令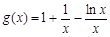 ,可得
,可得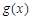 在
在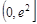 上递减,在
上递减,在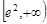 上递增,
上递增,
∴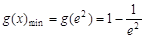 ,即
,即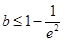 .------- 7分
.------- 7分
(Ⅲ)由(Ⅱ)知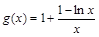 在(0,e2)上单调减
在(0,e2)上单调减
∴0<x<y<e2时,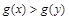 即
即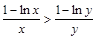
当0<x<e时,1-lnx>0,∴y(1-lnx)>x(1-lny), ∴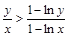
当e<x<e2时,1-lnx<0,∴y(1-lnx)>x(1-lny), ∴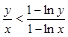 -----12分
-----12分
考点:利用函数的导数求极值最值单调区间
点评:不等式恒成立问题常转化为求函数最值问题。

练习册系列答案
相关题目
武汉市某地西瓜从2012年6月1日起开始上市。通过市场调查,得到西瓜种植成本Q(单位:元/ kg)与上市时间t(单位:天)的数据如下表:
kg)与上市时间t(单位:天)的数据如下表:
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
Q=at+b, Q=
 , Q= a
, Q= a , Q=a
, Q=a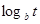 .
.2)利用你选取的函数,求西瓜种植成本最低时的上市天数及最低种植成本。

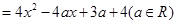 ,若方程
,若方程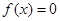 有两个均小于2的不同的实数根,则此时关于
有两个均小于2的不同的实数根,则此时关于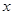 的不等式
的不等式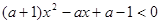 是否对一切实数
是否对一切实数 是奇函数:
是奇函数: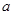 和
和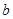 的值;
的值; 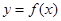 在区间
在区间 上的单调递减
上的单调递减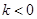 且不等式
且不等式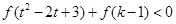 对任意的
对任意的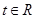 恒成立,求实数
恒成立,求实数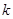 的取值范围.
的取值范围. 对于其定义域内的某一数
对于其定义域内的某一数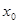 ,有
,有 ,则称
,则称 .
.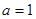 ,
,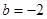 时,求函数
时,求函数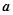 的取值范围;
的取值范围; 图象上两个点A、B的横坐标是函数
图象上两个点A、B的横坐标是函数 的图象上,求实数b的最小值.
的图象上,求实数b的最小值.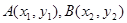 ,则线段AB的中点坐标为
,则线段AB的中点坐标为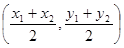 )
)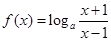 .
.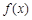 的定义域;(2)判断
的定义域;(2)判断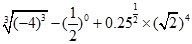 ; (2)
; (2)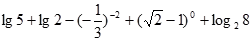 .
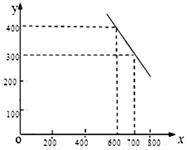
.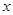 (元/件)之间,可近似看做一次函数
(元/件)之间,可近似看做一次函数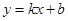 的关系(图象如图所示).
的关系(图象如图所示).