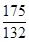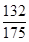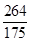题目内容
(本小题满分10分)
已知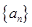 是等差数列,其中
是等差数列,其中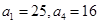 ]
]
(1)求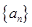 的通项;
的通项;
(2)数列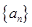 从哪一项开始小于0;
从哪一项开始小于0;
(3)求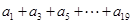 值。]
值。]
已知
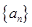 是等差数列,其中
是等差数列,其中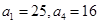 ]
](1)求
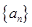 的通项;
的通项; (2)数列
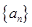 从哪一项开始小于0;
从哪一项开始小于0;(3)求
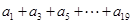 值。]
值。](1)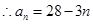 (2)从第10项开始小于0(3)-20
(2)从第10项开始小于0(3)-20
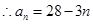 (2)从第10项开始小于0(3)-20
(2)从第10项开始小于0(3)-20试题分析:解:(1)
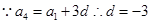
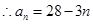
(2)
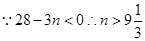 ∴数列
∴数列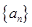 从第10项开始小于0
从第10项开始小于0 (3)
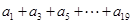 是首项为25,公差为
是首项为25,公差为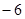 的等差数列,共有10项
的等差数列,共有10项 其和
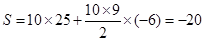
点评:解决该试题的关键是对于等差数列的前n项和的最值可以结合二次函数性质来得到,同时能结合公式求解结论。属于基础题。

练习册系列答案
相关题目
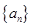 ,
,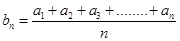 (
(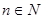 ),求证:
),求证: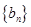 仍为等差数列;
仍为等差数列;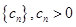
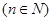 ),类比上述性质,写出一个真命题并加以证明.
),类比上述性质,写出一个真命题并加以证明.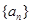 的通项
的通项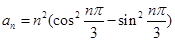 ,其前
,其前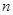 项和为
项和为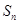 ,则
,则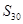 为 .
为 . 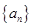 满足:
满足: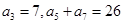 .
.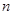 项和为
项和为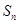 。
。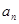 及
及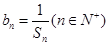 ,求数列
,求数列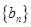 的前
的前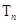 并证明
并证明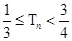 .
.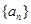 中,若
中,若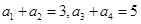 ,则
,则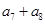 的和等于 ( )
的和等于 ( )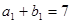 ,
,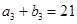 ,则
,则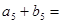 _________
_________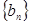 满足:
满足: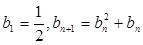 。
。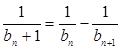 ;
;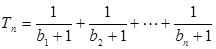 ,对任意的正整数
,对任意的正整数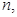
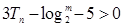 恒成立,求
恒成立,求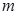 的取值范围。
的取值范围。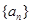 是等差数列,
是等差数列,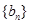 是公比为
是公比为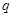 的等比数列,
的等比数列,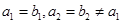 ,记
,记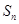 为数列
为数列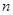 项和,
项和,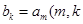 是大于
是大于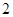 的正整数
的正整数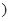 ,求证:
,求证: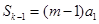 ;
;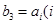 是某一正整数
是某一正整数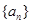 的通项公式
的通项公式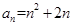 ,则数列
,则数列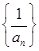 的前10项和为
的前10项和为