题目内容
已知y=f(x)函数的图象是由y=sinx的图象经过如下三步变换得到的:①将y=sinx的图象整体向左平移
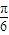 个单位;
个单位;②将①中的图象的纵坐标不变,横坐标缩短为原来的
 ;
;③将②中的图象的横坐标不变,纵坐标伸长为原来的2倍.
(1)求f(x)的周期和对称轴;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(C)=2,c=1,ab=2
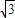 ,且a>b,求a,b的值.
,且a>b,求a,b的值.
【答案】分析:将y=sinx向左平移 个单位,得到y=sin(x+
个单位,得到y=sin(x+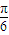 ),纵坐标不变,横坐标缩短为原来的
),纵坐标不变,横坐标缩短为原来的 ,变形为y=sin(2x+
,变形为y=sin(2x+ ),横坐标不变,纵坐标伸长为原来的2倍,变形为y=2sin(2x+
),横坐标不变,纵坐标伸长为原来的2倍,变形为y=2sin(2x+ ),得到f(x)的解析式,
),得到f(x)的解析式,
(1)找出ω的值,代入周期公式,即可求出f(x)的最小正周期;根据正弦函数的对称轴为kπ+ ,k∈Z,列出关于x的方程,求出方程的解得到f(x)的对称轴;
,k∈Z,列出关于x的方程,求出方程的解得到f(x)的对称轴;
(2)由f(C)=2,将x=C代入f(x)解析式中,使其值等于2,整理后根据C为三角形的内角,利用特殊角的三角函数值,求出C的度数,利用余弦定理得到c2=a2+b2-2abcosC,利用完全平方公式变形后,将c,cosC及ab的值代入,求出a2+b2=7,与ab=2 联立,根据a大于b,即可求出a与b的值.
联立,根据a大于b,即可求出a与b的值.
解答:解:(Ⅰ)由变换得:f(x)=2sin(2x+ ),
),
∵ω=2,
∴T= =π;
=π;
由2x+ =kπ+
=kπ+ ,k∈Z,得对称轴为x=
,k∈Z,得对称轴为x=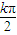 +
+ ,k∈Z;
,k∈Z;
(Ⅱ)由f(C)=2得:2sin(2C+ )=2,即sin(2C+
)=2,即sin(2C+ )=1,
)=1,
又C为三角形内角,
∴2C+ =
= ,即C=
,即C= ,
,
∴cosC= ,又c=1,ab=2
,又c=1,ab=2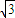 ,
,
在△ABC中,根据余弦定理,有c2=1=a2+b2-2abcosC=a2+b2-2×2 ×
× ,
,
整理得:a2+b2=7,与ab=2 联立,且a>b,
联立,且a>b,
解得:a=2,b=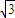 .
.
点评:此题属于解三角形的题型,涉及的知识有:余弦定理,三角函数的图象变换,三角函数的周期性及其求法,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.
 个单位,得到y=sin(x+
个单位,得到y=sin(x+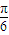 ),纵坐标不变,横坐标缩短为原来的
),纵坐标不变,横坐标缩短为原来的 ,变形为y=sin(2x+
,变形为y=sin(2x+ ),横坐标不变,纵坐标伸长为原来的2倍,变形为y=2sin(2x+
),横坐标不变,纵坐标伸长为原来的2倍,变形为y=2sin(2x+ ),得到f(x)的解析式,
),得到f(x)的解析式,(1)找出ω的值,代入周期公式,即可求出f(x)的最小正周期;根据正弦函数的对称轴为kπ+
 ,k∈Z,列出关于x的方程,求出方程的解得到f(x)的对称轴;
,k∈Z,列出关于x的方程,求出方程的解得到f(x)的对称轴;(2)由f(C)=2,将x=C代入f(x)解析式中,使其值等于2,整理后根据C为三角形的内角,利用特殊角的三角函数值,求出C的度数,利用余弦定理得到c2=a2+b2-2abcosC,利用完全平方公式变形后,将c,cosC及ab的值代入,求出a2+b2=7,与ab=2
 联立,根据a大于b,即可求出a与b的值.
联立,根据a大于b,即可求出a与b的值.解答:解:(Ⅰ)由变换得:f(x)=2sin(2x+
 ),
),∵ω=2,
∴T=
 =π;
=π;由2x+
 =kπ+
=kπ+ ,k∈Z,得对称轴为x=
,k∈Z,得对称轴为x=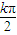 +
+ ,k∈Z;
,k∈Z;(Ⅱ)由f(C)=2得:2sin(2C+
 )=2,即sin(2C+
)=2,即sin(2C+ )=1,
)=1,又C为三角形内角,
∴2C+
 =
= ,即C=
,即C= ,
,∴cosC=
 ,又c=1,ab=2
,又c=1,ab=2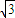 ,
,在△ABC中,根据余弦定理,有c2=1=a2+b2-2abcosC=a2+b2-2×2
 ×
× ,
,整理得:a2+b2=7,与ab=2
 联立,且a>b,
联立,且a>b,解得:a=2,b=
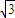 .
.点评:此题属于解三角形的题型,涉及的知识有:余弦定理,三角函数的图象变换,三角函数的周期性及其求法,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<1,则 个单位;
个单位; ;
; ,且a>b,求a,b的值.
,且a>b,求a,b的值.