题目内容
定义在R上的函数f（x）满足f（4）=1，f′（x）为f（x）的导函数，已知y=f′（x）的图象如图所示，若两个正数a、b满足f（2a+b）＜1，则| b+1 |
| a+1 |
(
，5)
| 1 |
| 3 |
(
，5)
．| 1 |
| 3 |
分析：先根据导函数的图象判断原函数的单调性，从而确定a、b的范围，最后利用不等式的性质得到答案．
解答：解：由图可知，当x＜0时，导函数f'（x）＜0，原函数单调递减，
∵两正数a，b满足f（2a+b）＜1，f（4）=1，
∴a，b满足
，
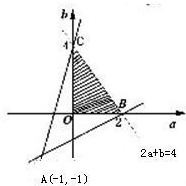
∴点（a，b）的区域为图中阴影部分，不包括边界，
的几何意义是区域的点与A（-1，-1）连线的斜率，
直线AB，AC的斜率分别是kAB=
，kAC=5，
∴
∈（
，5）．
故答案为：（
，5）．
∵两正数a，b满足f（2a+b）＜1，f（4）=1，
∴a，b满足
|
∴点（a，b）的区域为图中阴影部分，不包括边界，
| b+1 |
| a+1 |
直线AB，AC的斜率分别是kAB=
| 1 |
| 3 |
∴
| b+1 |
| a+1 |
| 1 |
| 3 |
故答案为：（
| 1 |
| 3 |
点评：本题主要考查函数的单调性与其导函数的正负之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．
练习册系列答案
科学实验活动册系列答案
相关题目