题目内容
【题目】已知![]() (
(![]() 是常数,
是常数,![]() ).
).
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若函数![]() 恰有两个不同的零点,求实数
恰有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1){![]() |
|![]() 或
或![]() };(2)
};(2)![]()
【解析】
(1)当a=1时,f(x)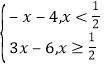 ,把
,把 或
或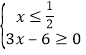 的解集取并集,即得所求;
的解集取并集,即得所求;
②由f(x)=0得|2x﹣1|=﹣ax+5,作出y=|2x﹣1|和y=﹣ax+5 的图象,观察可以知道,当﹣2<a<2时,这两个函数的图象有两个不同的交点,由此得到a的取值范围.
(1)当![]() 时,
时,![]() =
=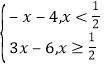 ,
,
由![]() ,得
,得 或
或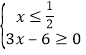 ,
,
解得![]() 或
或![]() ,
,
故不等式![]() 的解集为{
的解集为{![]() |
|![]() 或
或![]() }.
}.
(2)令![]() =0,得
=0,得![]() ,
,
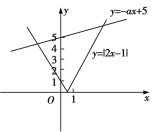
则函数![]() 恰有两个不同的零点转化为
恰有两个不同的零点转化为![]() 与
与![]() 的图象有两个不同的交点,在同一平面直角坐标系中作出两函数的图象如图所示,结合图象知当
的图象有两个不同的交点,在同一平面直角坐标系中作出两函数的图象如图所示,结合图象知当![]() 时,这两个函数的图象有两个不同的交点,所以当
时,这两个函数的图象有两个不同的交点,所以当![]() 时,函数
时,函数![]() 恰有两个不同的零点,故实数
恰有两个不同的零点,故实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
