题目内容
已知x=1是函数f(x)=mx3-3(m+1)x2+nx+1的一个极值点,其中m,n∈R,m<0.
(I)求m与n的关系表达式;
(II)求f(x)的单调区间.
解:(I)f′(x)=3mx2-6(m+1)x+n,
因为x=1是f(x)的一个极值点,
所以f′(1)=0,即3m-6(m+1)+n=0,所以n=3m+6.
(II)由(I)知,
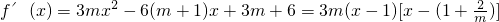 .
.
当m<0时,有 ,当x变化时,f(x)与f'(x)的变化如下表:
,当x变化时,f(x)与f'(x)的变化如下表:
由上表知,当m<0时,f(x)在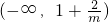 单调递减,
单调递减,
在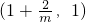 单调递增,(1+∞)单调递减.
单调递增,(1+∞)单调递减.
分析:(I)由x=1是函数f(x)=mx3-3(m+1)x2+nx+1的一个极值点,求导,则f′(1)=0,求得m与n的关系表达式;
(II)根据(I),代入f(x)中,求导,令导数f′(x)>0,求得单调增区间,令f′(x)<0,求得单调减区间.
点评:考查利用导数研究函数的单调区间和极值问题,求函数的单调区间实质是解不等式,属中档题.
因为x=1是f(x)的一个极值点,
所以f′(1)=0,即3m-6(m+1)+n=0,所以n=3m+6.
(II)由(I)知,
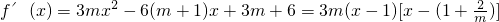 .
.当m<0时,有
 ,当x变化时,f(x)与f'(x)的变化如下表:
,当x变化时,f(x)与f'(x)的变化如下表:| x | 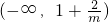 | 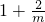 | 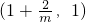 | 1 | (1,+∞) |
| f′(x) | <0 | 0 | >0 | 0 | <0 |
| f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
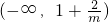 单调递减,
单调递减,在
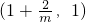 单调递增,(1+∞)单调递减.
单调递增,(1+∞)单调递减.分析:(I)由x=1是函数f(x)=mx3-3(m+1)x2+nx+1的一个极值点,求导,则f′(1)=0,求得m与n的关系表达式;
(II)根据(I),代入f(x)中,求导,令导数f′(x)>0,求得单调增区间,令f′(x)<0,求得单调减区间.
点评:考查利用导数研究函数的单调区间和极值问题,求函数的单调区间实质是解不等式,属中档题.

练习册系列答案
相关题目