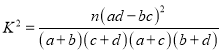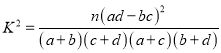题目内容
【题目】一缉私艇发现在方位角45°方向,距离12海里的海面上有一走私船正以10海里/小时的速度沿方位角为105°方向逃窜,若缉私艇的速度为14海里/小时,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追击所需时间和α角的正弦.(注:方位角是指正北方向按顺时针方向旋转形成的角,设缉私艇与走私船原来的位置分别为A、C,在B处两船相遇). 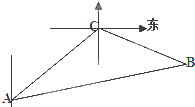
【答案】解:由条件知∠ACB=120°,AC=12海里,
设缉私船t小时后追上该走私船,可得BC=10t,AB=14t,
∴由正弦定理 ![]() =
= ![]() 得:
得: ![]() =
= ![]() ,
,
∴sinα= ![]() ,
,
由余弦定理AB2=AC2+BC2﹣2ACBCcos∠ACB得:(14t)2=122+(10t)2﹣240tcos120°,
解得:t=2或t=﹣ ![]() (舍),
(舍),
∴t=2小时,sinα= ![]() .
.
【解析】缉私艇与走私船原来的位置分别为A、C,在B处两船相遇,由条件得到∠ACB=120°,AC=12海里,设缉私船t小时后追上该走私船,根据各自的速度表示出BC与AB,由∠ACB=120°,∠CAB=α,利用正弦定理列出关系式,求出sinα的值;由余弦定理列出关于t的方程,求出方程的解即可得到t的值.
【考点精析】通过灵活运用正弦定理的定义,掌握正弦定理:![]() 即可以解答此题.
即可以解答此题.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】在一次爱心捐款活动中,小李为了了解捐款数额是否和居民自身的经济收入有关,随机调査了某地区的![]() 个捐款居民每月平均的经济收入. 在捐款超过
个捐款居民每月平均的经济收入. 在捐款超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个,达到
个,达到![]() 元的有
元的有![]() 个;在捐款不超过
个;在捐款不超过![]() 元的居民中,每月平均的经济收入没有达到
元的居民中,每月平均的经济收入没有达到![]() 元的有
元的有![]() 个.
个.
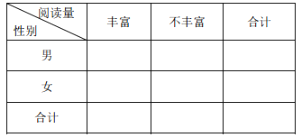
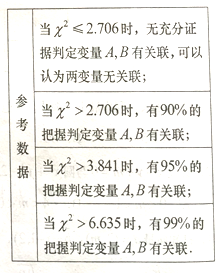
(1)在下图表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否超过
以上的把握认为捐款数额是否超过![]() 元和居民毎月平均的经济收入是否达到
元和居民毎月平均的经济收入是否达到![]() 元有关?
元有关?
(2)将上述调查所得到的频率视为概率. 现在从该地区大量居民中,采用随机抽样方法毎次抽取![]() 个居民,共抽取
个居民,共抽取![]() 次,记被抽取的
次,记被抽取的![]() 个居民中经济收入达到
个居民中经济收入达到![]() 元的人数为
元的人数为![]() ,求
,求![]() 和期望
和期望![]() 的值.
的值.
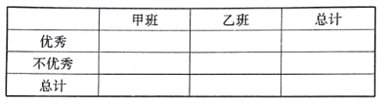
每月平均经济收入达到 | 每月平均经济收入没有达到 | 合计 | |
捐款超过 | |||
捐款不超过 | |||
合计 |
附: 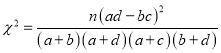 ,其中
,其中![]()
【题目】某网站针对2015年中国好声音歌手A,B,C三人进行网上投票,结果如下
观众年龄 | 支持A | 支持B | 支持C |
20岁以下 | 100 | 200 | 600 |
20岁以上(含20岁) | 100 | 100 | 400 |
(1)在所有参与该活动的人中,用分层抽样的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分层抽样的方法抽取5人作为一个总体,从这5人中任意选取2人,求恰有1人在20岁以下的概率.