题目内容
12.已知p,q满足p+2q-1=0,则直线px+3y+q=0必过定点( )| A. | $(-\frac{1}{6},\frac{1}{2})$ | B. | $(\frac{1}{2},\frac{1}{6})$ | C. | $(\frac{1}{2},-\frac{1}{6})$ | D. | $(\frac{1}{6},-\frac{1}{2})$ |
分析 消元整理可得x+3y+q(1-2x)=0,由直线系的知识解方程组可得.
解答 解:∵p,q满足p+2q-1=0,∴p=1-2q,
代入直线方程px+3y+q=0可得(1-2q)x+3y+q=0,
整理可得x+3y+q(1-2x)=0,
解方程组$\left\{\begin{array}{l}{x+3y=0}\\{1-2x=0}\end{array}\right.$可得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{1}{6}}\end{array}\right.$,
∴直线px+3y+q=0必过定点($\frac{1}{2}$,-$\frac{1}{6}$)
故选:C.
点评 本题考查直线系方程,涉及消元思想和方程组的解法,属基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
17.设A={3},B={3,5},则下列表达关系不正确的是( )
| A. | A?B | B. | A⊆B | C. | 3∈B | D. | 5⊆B |
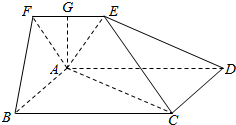 如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,G是EF的中点,AG=1
如图,在五面体ABCDEF中,四边形ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,G是EF的中点,AG=1