题目内容
将函数y=3sin(x-θ)的图象F按向量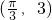 平移得到图象F',若F'的一条对称轴是直线
平移得到图象F',若F'的一条对称轴是直线 ,则θ的一个可能取值是
,则θ的一个可能取值是
- A.

- B.
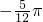
- C.
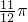
- D.
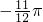
A
分析:由题意可得图象F'对应的解析式为 y═3sin[(x- )-θ]+3,由F'的一条对称轴是直线
)-θ]+3,由F'的一条对称轴是直线 ,则
,则
3sin[( -
- )-θ]+3 取得最值,由-
)-θ]+3 取得最值,由- -θ=kπ+
-θ=kπ+ ,k∈z,求出 θ的值.
,k∈z,求出 θ的值.
解答:函数y=3sin(x-θ)的图象F按向量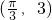 平移得到图象F',
平移得到图象F',
故图象F'对应的解析式为 y═3sin[(x- )-θ]+3.
)-θ]+3.
若F'的一条对称轴是直线 ,则3sin[(
,则3sin[( -
- )-θ]+3 取得最值.
)-θ]+3 取得最值.
∴- -θ=kπ+
-θ=kπ+ ,k∈z,故 θ=-kπ-
,k∈z,故 θ=-kπ- ,k∈z,即 θ=nπ-
,k∈z,即 θ=nπ- ,n∈z.
,n∈z.
故选A.
点评:本题主要考查三角函数的对称性,函数y=Asin(ωx+∅)的图象变换,属于中档题.
分析:由题意可得图象F'对应的解析式为 y═3sin[(x-
 )-θ]+3,由F'的一条对称轴是直线
)-θ]+3,由F'的一条对称轴是直线 ,则
,则3sin[(
 -
- )-θ]+3 取得最值,由-
)-θ]+3 取得最值,由- -θ=kπ+
-θ=kπ+ ,k∈z,求出 θ的值.
,k∈z,求出 θ的值.解答:函数y=3sin(x-θ)的图象F按向量
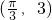 平移得到图象F',
平移得到图象F',故图象F'对应的解析式为 y═3sin[(x-
 )-θ]+3.
)-θ]+3.若F'的一条对称轴是直线
 ,则3sin[(
,则3sin[( -
- )-θ]+3 取得最值.
)-θ]+3 取得最值.∴-
 -θ=kπ+
-θ=kπ+ ,k∈z,故 θ=-kπ-
,k∈z,故 θ=-kπ- ,k∈z,即 θ=nπ-
,k∈z,即 θ=nπ- ,n∈z.
,n∈z.故选A.
点评:本题主要考查三角函数的对称性,函数y=Asin(ωx+∅)的图象变换,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目