题目内容
15.已知a>0,b>0,2a,$\sqrt{2}$,2b成等比数列,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为4.分析 由题意和等比数列可得a+b=1,进而可得$\frac{1}{a}$+$\frac{1}{b}$=($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=2+$\frac{b}{a}$+$\frac{a}{b}$,由基本不等式可得.
解答 解:∵a>0,b>0,2a,$\sqrt{2}$,2b成等比数列,
∴($\sqrt{2}$)2=2a•2b=2a+b,∴a+b=1
∴$\frac{1}{a}$+$\frac{1}{b}$=($\frac{1}{a}$+$\frac{1}{b}$)(a+b)
=2+$\frac{b}{a}$+$\frac{a}{b}$≥2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=4
当且仅当$\frac{b}{a}$=$\frac{a}{b}$即a=b=$\frac{1}{2}$时取等号,
故答案为:4
点评 本题考查基本不等式求最值,属解等比数列的通项公式,属基础题.

练习册系列答案
相关题目
7.已知cosα=$\frac{3}{5}$,sin β=-$\frac{5}{13}$,且α∈(0,$\frac{π}{2}$),β∈(-$\frac{π}{2}$,0),则sin(α+β)=( )
| A. | $\frac{33}{65}$ | B. | $\frac{63}{65}$ | C. | $\frac{33}{65}$或-$\frac{33}{65}$ | D. | -$\frac{63}{65}$ |
10.已知△ABC中,a=2$\sqrt{2}$,b=2$\sqrt{3}$,B=60°,那么角sinA等于( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
 甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时).图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图象(线段AB表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时).图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图象(线段AB表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题: 是偶函数,且当
是偶函数,且当 时,
时,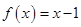 ,则不等式
,则不等式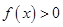 的解集是( )
的解集是( )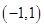 B.
B.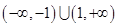
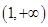 D.
D.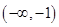
 的通项公式
的通项公式 ,设其前
,设其前 项和为
项和为 ,则使
,则使 成立的自然数
成立的自然数 有( )
有( )