题目内容
甲箱中放有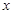 个红球与
个红球与 个白球(
个白球( ,且
,且 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
(Ⅰ)记取出的3个球颜色全不相同的概率为 ,求当
,求当 取得最大值时的
取得最大值时的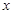 ,
, 的值;
的值;
(Ⅱ)当 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数 的期望
的期望 。
。
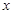 个红球与
个红球与 个白球(
个白球( ,且
,且 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。(Ⅰ)记取出的3个球颜色全不相同的概率为
 ,求当
,求当 取得最大值时的
取得最大值时的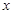 ,
, 的值;
的值;(Ⅱ)当
 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数 的期望
的期望 。
。 (Ⅰ) (Ⅱ)分布列见解析,数学期望为
(Ⅱ)分布列见解析,数学期望为
 (Ⅱ)分布列见解析,数学期望为
(Ⅱ)分布列见解析,数学期望为
本试题主要是考查了古典概型概率的运算,以及分布列的求解和运用。
(1)根据题目中的条件表示概率值,结合均值不等式得到最值。
(2)先求解随机变量的各个取值的概率值,然后结合分布列而后数学期望值公式得到结论。解:(Ⅰ)由题意知
 2分
2分
当且仅当 时等号成立
时等号成立
所以,当 取得最大值时,
取得最大值时,
 3分
3分
(Ⅱ)当 时,甲箱中有2个红球与4个白球。
时,甲箱中有2个红球与4个白球。
而 的所有可能取值为0,1,2,3
的所有可能取值为0,1,2,3
则



所以,红球个数 的分布列为:
的分布列为:
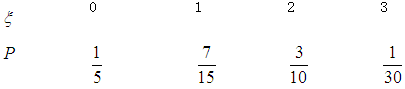 7分
7分
于是
 8分
8分
(1)根据题目中的条件表示概率值,结合均值不等式得到最值。
(2)先求解随机变量的各个取值的概率值,然后结合分布列而后数学期望值公式得到结论。解:(Ⅰ)由题意知
 2分
2分当且仅当
 时等号成立
时等号成立所以,当
 取得最大值时,
取得最大值时, 3分
3分(Ⅱ)当
 时,甲箱中有2个红球与4个白球。
时,甲箱中有2个红球与4个白球。而
 的所有可能取值为0,1,2,3
的所有可能取值为0,1,2,3则




所以,红球个数
 的分布列为:
的分布列为: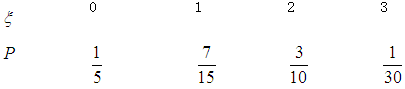 7分
7分于是
 8分
8分
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min. 的分布列及期望.
的分布列及期望. 的分布列和数学期望.
的分布列和数学期望. 



 ,求
,求 (元)的概率分布列和期望
(元)的概率分布列和期望 .
. 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望; ,k=1,2,3,则D(3X +5)等于 ( )
,k=1,2,3,则D(3X +5)等于 ( )