题目内容
．（本小题10分）
在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券中任抽2张，求：（1）该顾客中奖的概率；（2）该顾客获得的奖品总价值
（元）的概率分布列和期望
.
在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券中任抽2张，求：（1）该顾客中奖的概率；（2）该顾客获得的奖品总价值
（元）的概率分布列和期望.（1）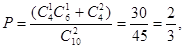
（2）由于10张券总价值为80元，即每张的平均奖品价值为8元，从而抽2张的平均奖品价值=2×8=16（元）.
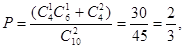（2）由于10张券总价值为80元，即每张的平均奖品价值为8元，从而抽2张的平均奖品价值=2×8=16（元）.本题考查等可能事件的概率和互斥事件的概率，本题解题的关键是看出要求概率的事件包含的结果数比较多，注意做到不重不漏．
（1）本题是一个等可能事件的概率，而顾客中奖的对立事件是顾客不中奖，从10张中抽2张有C102种结果，抽到的不中奖有C62种结果，得到概率
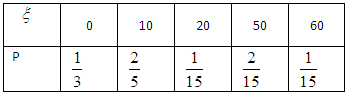
（2）的所有可能值为：0，10，20，50，60（元）然后接合古典概型得到概率值，求解分布列。．
解法一：
（1）
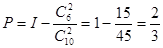，即该顾客中奖的概率为
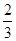. -----------3分
（2）的所有可能值为：0，10，20，50，60（元）. -----------4分
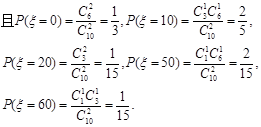-----------7分
故有分布列：----------9分
从而期望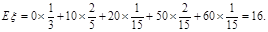
----------10分
解法二：
（1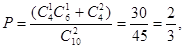）（2）的分布列求法同解法一
由于10张券总价值为80元，即每张的平均奖品价值为8元，从而抽2张的平均奖品价值=2×8=16（元）.
（1）本题是一个等可能事件的概率，而顾客中奖的对立事件是顾客不中奖，从10张中抽2张有C102种结果，抽到的不中奖有C62种结果，得到概率
（2）
的所有可能值为：0，10，20，50，60（元）然后接合古典概型得到概率值，求解分布列。．解法一：
（1）
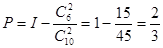，即该顾客中奖的概率为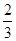. -----------3分（2）
的所有可能值为：0，10，20，50，60（元）. -----------4分 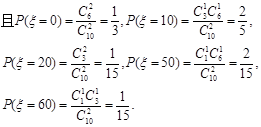-----------7分故
有分布列：----------9分从而期望
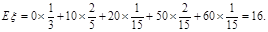----------10分解法二：
（1）
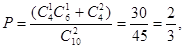（2）的分布列求法同解法一由于10张券总价值为80元，即每张的平均奖品价值为8元，从而抽2张的平均奖品价值
=2×8=16（元）.
练习册系列答案
小学期末标准试卷系列答案
相关题目
．
为在体操岗位服务的美国志愿者的个数，求
（
、
.根据教练员提供的资料，其概率分布如下表:
个红球与
个白球（
，且
），乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球，从乙箱中任取1个球。
，求当
时，求取出的3个球中红球个数
的期望
。
，（已知甲回答每个问题的正确率相同，并且相互之间没有影响。）（I）求甲选手回答一个问题的正确率；（Ⅱ）求选手甲可进入决赛的概率；（Ⅲ）设选手甲在初赛中答题的个数为
，试写出
四个不同的岗位服务，每个岗位至少有一名志愿者，设随机变量
为这五名志愿者中参加
岗位服务的人数，则
＿
