题目内容
(本小题满分12分)在我校值周活动中,甲、乙等五名值周生被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名值周生.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量X为这五名值周生中参加A岗位服务的人数,求X的分布列及期望.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量X为这五名值周生中参加A岗位服务的人数,求X的分布列及期望.
(1)甲、乙两人同时参加A岗位服务的概率是 .
.
(2)甲、乙两人不在同一岗位服务的概率是P( )=1-P(F)=
)=1-P(F)= .
.
(3)X的分布列为:

期望为 。
。
 .
.(2)甲、乙两人不在同一岗位服务的概率是P(
 )=1-P(F)=
)=1-P(F)= .
.(3)X的分布列为:

期望为
 。
。本题考查等可能事件的概率,解题的关键是看清试验发生包含的事件数和满足条件的事件数,可以用排列组合表示出来,有的题目还可以列举出所有结果
(Ⅰ)本题是一个等可能事件的概率,试验发生包含的事件数 ,满足条件的事件是甲、乙两人同时参加A岗位服务有
,满足条件的事件是甲、乙两人同时参加A岗位服务有 种结果,得到概率.
种结果,得到概率.
(Ⅱ)由题意知本题是一个等可能事件的概率,试验发生包含的事件数 ,满足条件的事件数是4个元素的全排列,得到概率.
,满足条件的事件数是4个元素的全排列,得到概率.
(Ⅲ)随机变量ξ可能取的值为1,2.事件ξ=2是指有两人同时参加A岗位服务,根据等可能事件的概率公式得到结果,然后用1减去得到变量等于1的概率.
解:(1)记甲、乙两人同时参加A岗位服务为事件E,那么P(E)= =
= .
.
即甲、乙两人同时参加A岗位服务的概率是 .
.
(2)记甲、乙两人同时参加同一岗位服务为事件F,那么P(F)= =
= .
.
所以,甲、乙两人不在同一岗位服务的概率是P( )=1-P(F)=
)=1-P(F)= .
.
(3)随机变量X可能取的值为1,2,事件“X=2”是指有两人同时参加A岗位服务,则P(X=2)= =
= .所以P(X=1)=1-P(X=2)=
.所以P(X=1)=1-P(X=2)= ,X的分布列为:
,X的分布列为:

期望为 。
。
(Ⅰ)本题是一个等可能事件的概率,试验发生包含的事件数
 ,满足条件的事件是甲、乙两人同时参加A岗位服务有
,满足条件的事件是甲、乙两人同时参加A岗位服务有 种结果,得到概率.
种结果,得到概率.(Ⅱ)由题意知本题是一个等可能事件的概率,试验发生包含的事件数
 ,满足条件的事件数是4个元素的全排列,得到概率.
,满足条件的事件数是4个元素的全排列,得到概率.(Ⅲ)随机变量ξ可能取的值为1,2.事件ξ=2是指有两人同时参加A岗位服务,根据等可能事件的概率公式得到结果,然后用1减去得到变量等于1的概率.
解:(1)记甲、乙两人同时参加A岗位服务为事件E,那么P(E)=
 =
= .
.即甲、乙两人同时参加A岗位服务的概率是
 .
.(2)记甲、乙两人同时参加同一岗位服务为事件F,那么P(F)=
 =
= .
.所以,甲、乙两人不在同一岗位服务的概率是P(
 )=1-P(F)=
)=1-P(F)= .
.(3)随机变量X可能取的值为1,2,事件“X=2”是指有两人同时参加A岗位服务,则P(X=2)=
 =
= .所以P(X=1)=1-P(X=2)=
.所以P(X=1)=1-P(X=2)= ,X的分布列为:
,X的分布列为:
期望为
 。
。
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 .
. 为在体操岗位服务的美国志愿者的个数,求
为在体操岗位服务的美国志愿者的个数,求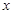 个红球与
个红球与 个白球(
个白球( ,且
,且 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。 ,求当
,求当 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数 的期望
的期望 。
。 ,
,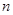 ,平均数为
,平均数为 ,则
,则 ( )
( ) 四个不同的岗位服务,每个岗位至少有一名志愿者,设随机变量
四个不同的岗位服务,每个岗位至少有一名志愿者,设随机变量 为这五名志愿者中参加
为这五名志愿者中参加 岗位服务的人数,则
岗位服务的人数,则 _
_ 表示4名乘客在第4层下电梯的人数,则
表示4名乘客在第4层下电梯的人数,则



 ,求
,求 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中: 的分布列与期望.
的分布列与期望.