Question

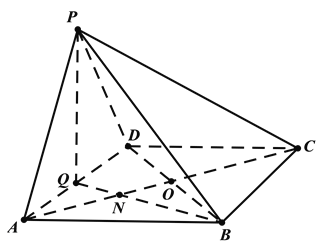
【题目】如图，在四棱锥P－ABCD中，底面ABCD为菱形，∠BAD＝60°，Q为AD的中点．

(1)若PA＝PD，求证：平面PQB⊥平面PAD；

(2)点M在线段PC上，PM＝tPC，试确定实数t的值，使得PA∥平面MQB.

Answer 1

【答案】（1）详见解析（2）PM＝PC，t＝.

【解析】试题分析：（1）要证平面平面，只要证平面，它可以由和得到．（2）中连接交于，交于，因为平面，故，由此可以得到，从而可以得到的大小．

解析：(1)证明：连结，四边形为菱形，∵， ，∴为正三角形， 为的中点，∴.∵ ， 为的中点， ． 又，∴平面， 平面，∴平面平面．

(2)当 时，使得平面，连接交于，交于，则为的中点．又∵为边的中线．∴为正三角形的中心. 令菱形的边长为a，则．∵平面， 平面，平面平面，∴， 即．