Question

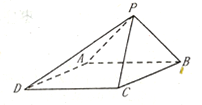
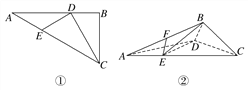
【题目】如图①所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连接AB，BE，如图②所示，设点F是AB的中点．

(1)求证：DE⊥平面BCD；

(2)若EF∥平面BDG，其中G为AC上一点，求三棱锥B－DEG的体积．

Answer 1

【答案】(1)见解析；(2)

【解析】试题分析：（1）先根据平几知识可得ED⊥DC.再由面面垂直性质定理得DE⊥平面BCD.（2）先根据线面平行性质定理得EF∥BG，G为EC的中点，由面面垂直性质定理得B到DC的距离就是三棱锥B－DEG的高，再根据锥体体积公式求体积

试题解析：(1)证明　取AC的中点P，连接DP，因为在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，

所以∠A＝30°，△ADC是等腰三角形，所以DP⊥AC，DP＝，∠DCP＝30°，∠PDC＝60°.

又点E在线段AC上，CE＝4，

所以AE＝2，EP＝1，所以∠EDP＝30°，

所以∠EDC＝90°，所以ED⊥DC.

因为平面BCD⊥平面ACD，且平面BCD∩平面ACD＝DC，所以DE⊥平面BCD.

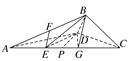
(2)解　若EF∥平面BDG，其中G为AC上一点，

则易知G为EC的中点，此时AE＝EG＝GC＝2.

因为在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，

所以BD＝，DC＝2，

所以B到DC的距离h＝＝＝.

因为平面BCD⊥平面ACD，平面BCD∩平面ACD＝DC，

所以B到DC的距离h就是三棱锥B－DEG的高，

所以三棱锥B－DEG的体积V＝·S△DEG·h＝××＝.