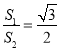题目内容
【题目】在平面直角坐标系![]() 中,已知圆心在
中,已知圆心在![]() 轴上,半径为2的圆
轴上,半径为2的圆![]() 位于
位于![]() 轴右侧,且与直线
轴右侧,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且
,且![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的
的坐标及对应的![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
【答案】(1)![]() (2)存在,点
(2)存在,点![]() 的坐标是
的坐标是![]() 与
与![]() ,对应面积的最大值为
,对应面积的最大值为![]()
【解析】
(1) 设圆心是![]() ,根据直线与圆相切的性质结合点到直线距离公式可以求出
,根据直线与圆相切的性质结合点到直线距离公式可以求出![]() 的值,也就可以写出圆
的值,也就可以写出圆![]() 的方程;
的方程;
(2) 根据点![]() 在圆
在圆![]() 上,可以求出
上,可以求出![]() 的取值范围,根据点到直线距离公式可以求出原点到直线
的取值范围,根据点到直线距离公式可以求出原点到直线![]() 的距离,利用垂径定理可以求出
的距离,利用垂径定理可以求出![]() ,最后求出
,最后求出![]() 的面积的表达式,最后利用配方法求出
的面积的表达式,最后利用配方法求出![]() 的面积最大.
的面积最大.
解(1)设圆心是![]() .
.
![]() 解得
解得![]()
![]() 圆
圆![]() 的方程为
的方程为![]() ;
;
(2)![]() 点
点![]() 在圆
在圆![]() ,
,
![]()
![]() .
.
又![]() 原点到直线
原点到直线![]() 的距离
的距离![]() 解得
解得![]()
![]() .
.
![]()
![]() .
.
![]() 当
当![]() ,即
,即![]() 时取得最大值
时取得最大值![]() .
.
此时点![]() 的坐标是
的坐标是![]() 与
与![]() ,面积的最大值为
,面积的最大值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店,为合理安排各地区加盟店的个数,先在其中5个地区试点,得到试点地区加盟店个数分别为1,2,3,4,5时,单店日平均营业额![]() (万元)的数据如下:
(万元)的数据如下:
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
(1)求单店日平均营业额![]() (万元)与所在地区加盟店个数
(万元)与所在地区加盟店个数![]() (个)的线性回归方程;
(个)的线性回归方程;
(2)根据试点调研结果,为保证规模和效益,在其他5个地区,该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元,求一个地区开设加盟店个数![]() 的所有可能取值;
的所有可能取值;
(3)小赵与小王都准备加入该公司的加盟店,根据公司规定,他们只能分别从其他五个地区(加盟店都不少于2个)中随机选一个地区加入,求他们选取的地区相同的概率.
(参考数据及公式:![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,其中
,其中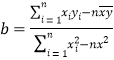 ,
,![]() .)
.)
【题目】![]() 年,在庆祝中华人民共和国成立
年,在庆祝中华人民共和国成立![]() 周年之际,又迎来了以“创军人荣耀,筑世界和平”为宗旨的第七届世界军人运动会.据悉,这次军运会将于
周年之际,又迎来了以“创军人荣耀,筑世界和平”为宗旨的第七届世界军人运动会.据悉,这次军运会将于![]() 年
年![]() 月
月![]() 日至
日至![]() 日在美丽的江城武汉举行,届时将有来自全世界
日在美丽的江城武汉举行,届时将有来自全世界![]() 多个国家和地区的近万名军人运动员参赛.相对于奥运会、亚运会等大型综合赛事,军运会或许对很多人来说还很陌生.为此,武汉某高校为了在学生中更广泛的推介普及军运会相关知识内容,特在网络上组织了一次“我所知晓的武汉军运会”知识问答比赛,为便于对答卷进行对比研究,组委会抽取了
多个国家和地区的近万名军人运动员参赛.相对于奥运会、亚运会等大型综合赛事,军运会或许对很多人来说还很陌生.为此,武汉某高校为了在学生中更广泛的推介普及军运会相关知识内容,特在网络上组织了一次“我所知晓的武汉军运会”知识问答比赛,为便于对答卷进行对比研究,组委会抽取了![]() 名男生和
名男生和![]() 名女生的答卷,他们的考试成绩频率分布直方图如下:
名女生的答卷,他们的考试成绩频率分布直方图如下:
(注:问卷满分为![]() 分,成绩
分,成绩![]() 的试卷为“优秀”等级)
的试卷为“优秀”等级)
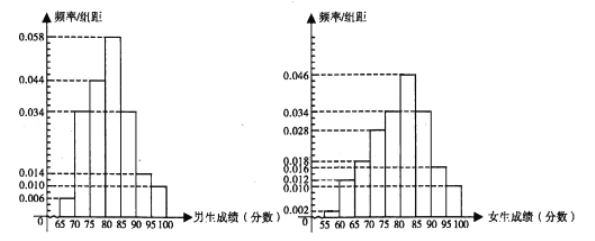
(1)从现有![]() 名男生和
名男生和![]() 名女生答卷中各取一份,分别求答卷成绩为“优秀”等级的概率;
名女生答卷中各取一份,分别求答卷成绩为“优秀”等级的概率;
(2)求列联表中![]() ,
,![]() ,
,![]() ,
,![]() 的值,并根据列联表回答:能否在犯错误的概率不超过
的值,并根据列联表回答:能否在犯错误的概率不超过![]() 的前提下认为“答卷成绩为优秀等级与性别有关”?
的前提下认为“答卷成绩为优秀等级与性别有关”?
男 | 女 | 总计 | |
优秀 |
|
|
|
非优秀 |
|
|
|
总计 |
|
|
|
(3)根据男、女生成绩频率分布直方图,对他们的成绩的优劣进行比较.
附:参考公式:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|