题目内容
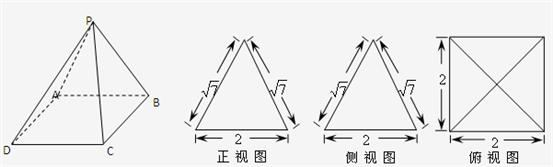
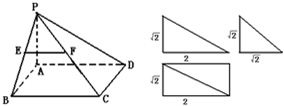 一个多面体的直观图和三视图如图所示,E,F分别为PB,PC中点.
一个多面体的直观图和三视图如图所示,E,F分别为PB,PC中点.(1)证明:EF∥平面PAD;
(2)求三棱锥E-ABC的体积.
分析:(1)由三视图可得PA⊥面ABCD,且ABCD 为矩形,由三角形的中位线的性质可得 EF∥BC,从而有EF∥AD,证得EF∥平面PAD.
(2)E到平面ABC的距离等于
PA,△ABC的面积等于矩形ABCD面积的一半,代入三棱锥的体积公式进行运算.
(2)E到平面ABC的距离等于
| 1 |
| 2 |
解答:解:(1)由三视图可得PA⊥面ABCD,且ABCD 为矩形,PA=
,AB=
,AD=2.
∵E,F分别为PB,PC中点,∴EF∥BC,∴EF∥AD,而 AD?平面PAD,EF不在平面PAD内,
故有 EF∥平面PAD.
(2)E到平面ABC的距离等于
PA=
,△ABC的面积为
AB•AD=
,
故三棱锥E-ABC的体积为
•(
AB•AD )•
PA=
•
•
=
.
| 2 |
| 2 |
∵E,F分别为PB,PC中点,∴EF∥BC,∴EF∥AD,而 AD?平面PAD,EF不在平面PAD内,
故有 EF∥平面PAD.
(2)E到平面ABC的距离等于
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
故三棱锥E-ABC的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
点评:本题考查证明线面平行的方法,三棱锥的体积公式,根据三视图判断几何体的形状是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
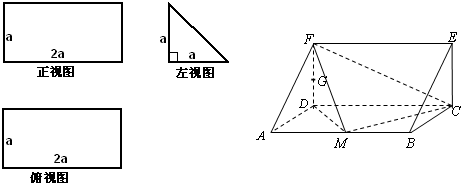
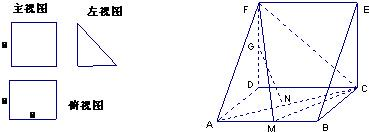 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.