题目内容
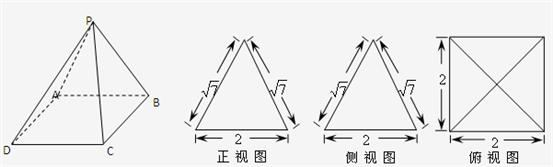
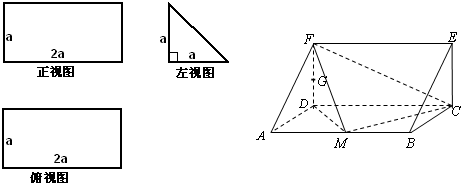
一个多面体的直观图和三视图如图所示,其中M、G分别是AB、DF的中点.
(1)在AD上(含A、D端点)确定一点P,使得GP∥平面FMC;
(2)一只苍蝇在几何体ADF-BCE内自由飞翔,求它飞入几何体F-AMCD内的概率.

(1)在AD上(含A、D端点)确定一点P,使得GP∥平面FMC;
(2)一只苍蝇在几何体ADF-BCE内自由飞翔,求它飞入几何体F-AMCD内的概率.

分析:(1)由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC,点P在A点处,取FC中点S,连接GS、MS、GA,根据中位线定理可知GS∥AB且GS=
AB,从而得到四边形AGSM为平行四边形,可证得结论;
(2)先根据三棱锥的体积公式求出F-AMCD的体积与三棱锥的体积公式求出ADF-BCE的体积,最后根据几何概型的概率公式解之即可.
| 1 |
| 2 |
(2)先根据三棱锥的体积公式求出F-AMCD的体积与三棱锥的体积公式求出ADF-BCE的体积,最后根据几何概型的概率公式解之即可.
解答:(本小题满分12分).
解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC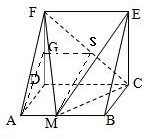
(1)点P在A点处.…(2分)
证明:取FC中点S,连接GS、MS、GA
∵G是DF的中点,
∴GS∥AB,且GS=
AB,
∴四边形AGSM为平行四边形
∴AG∥MS,而AG?平面FMC,MS?平面FMC
∴AG∥面FMC,
∴在AD上(含A、D端点)确定一点P即在A点处,使得GP∥平面FMC;
(2)因为VF-AMCD=
SAMCD×DF=
a3,
VADF-BCE=
a3,…(10分)
所以它飞入几何体F-AMCD内的概率为
=
…(12分)
解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC

(1)点P在A点处.…(2分)
证明:取FC中点S,连接GS、MS、GA
∵G是DF的中点,
∴GS∥AB,且GS=
| 1 |
| 2 |
∴四边形AGSM为平行四边形
∴AG∥MS,而AG?平面FMC,MS?平面FMC
∴AG∥面FMC,
∴在AD上(含A、D端点)确定一点P即在A点处,使得GP∥平面FMC;
(2)因为VF-AMCD=
| 1 |
| 3 |
| 1 |
| 4 |
VADF-BCE=
| 1 |
| 2 |
所以它飞入几何体F-AMCD内的概率为
| ||
|
| 1 |
| 2 |
点评:本题主要考查了线面垂直的判定,以及几何概型的应用,同时考查了空间想象能力和计算能力,属于中档题.

练习册系列答案
相关题目
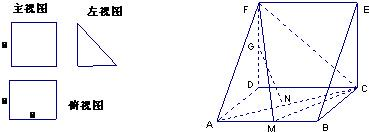 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.