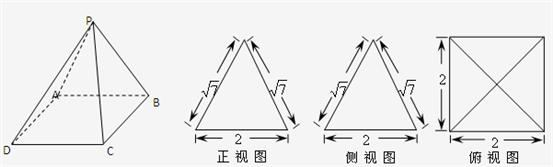
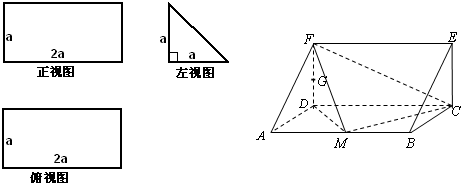
题目内容
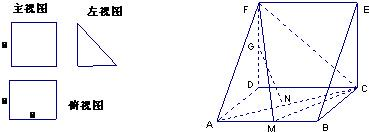 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.(Ⅰ)求证:GN⊥AC;
(Ⅱ)求二面角F-MC-D的正切值.
分析:(Ⅰ)连接DB,欲证GN⊥AC,只需证AC⊥面FDN,根据直线与平面垂直的判定定理可知只需证AC与面FDN内两相交直线垂直,而FD⊥AC,AC⊥DN,满足定理条件;
(Ⅱ)取BC中点R,连接DR交MC于Q,连接FQ,根据二面角平面角的定义可知∠DQF即为二面角F-MC-D的平面角,在Rt△DQF中求出此角的正切值即可.
(Ⅱ)取BC中点R,连接DR交MC于Q,连接FQ,根据二面角平面角的定义可知∠DQF即为二面角F-MC-D的平面角,在Rt△DQF中求出此角的正切值即可.
解答: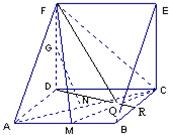 解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC.
解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC.
(Ⅰ)连接DB,可知B、N、D共线,且AC⊥DN.
又FD⊥AD,FD⊥CD,
∴FD⊥面ABCD.
∴FD⊥AC.
∴AC⊥面FDN,GN?面FDN.
∴GN⊥AC.
(Ⅱ)取BC中点R,连接DR交MC于Q,连接FQ.
在Rt△CDR和Rt△BCM中,CD=BC,RC=MB,
∴Rt△CDR≌和Rt△BCM,
∴∠RDC=∠BCM,而∠DCQ+∠BCM=90°
∴∠DCQ+∠RDC=90°,
∴RD⊥MC.
而FD⊥面ABCD,故FD⊥MC.
∴MC⊥面FDQ,
∴MC⊥FQ,
∴∠DQF即为二面角F-MC-D的平面角.
在Rt△CDR中,DR=
=
a.
由射影定理知,CD2=DQ•DR,得DQ=
=
.
在Rt△DQF中,tan∠DQF=
=
=
.
故二面角F-MC-D的正切值是
.
 解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC.
解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC.(Ⅰ)连接DB,可知B、N、D共线,且AC⊥DN.
又FD⊥AD,FD⊥CD,
∴FD⊥面ABCD.
∴FD⊥AC.
∴AC⊥面FDN,GN?面FDN.
∴GN⊥AC.
(Ⅱ)取BC中点R,连接DR交MC于Q,连接FQ.
在Rt△CDR和Rt△BCM中,CD=BC,RC=MB,
∴Rt△CDR≌和Rt△BCM,
∴∠RDC=∠BCM,而∠DCQ+∠BCM=90°
∴∠DCQ+∠RDC=90°,
∴RD⊥MC.
而FD⊥面ABCD,故FD⊥MC.
∴MC⊥面FDQ,
∴MC⊥FQ,
∴∠DQF即为二面角F-MC-D的平面角.
在Rt△CDR中,DR=
a2+(
|
| ||
| 2 |
由射影定理知,CD2=DQ•DR,得DQ=
| a2 | ||||
|
2
| ||
| 5 |
在Rt△DQF中,tan∠DQF=
| DF |
| DQ |
| a | ||||
|
| ||
| 2 |
故二面角F-MC-D的正切值是
| ||
| 2 |
点评:本题主要考查直三棱柱的有关知识,以及求二面角的问题,以及分析问题与解决问题的能力.简单几何体是立体几何解答题的主要载体,特别是棱柱和棱锥.由于棱锥已多次出现在高考试题中,估计今年高考会以棱柱为载体来命题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目