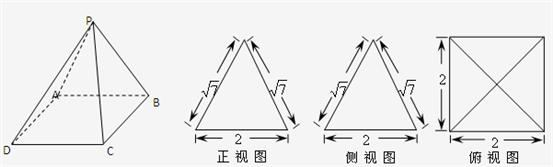
题目内容
一个多面体的直观图和三视图如图所示,其中M、G分别是AB、DF的中点.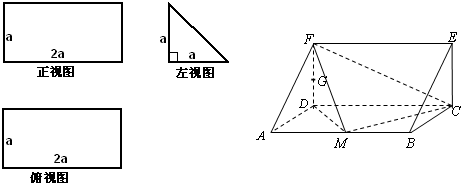
(1)求证:CM⊥平面FDM;
(2)在线段AD上(含A、D端点)确定一点P,使得GP∥平面FMC,并给出证明.
分析:(Ⅰ)因为直线FD⊥平面ABCD,CM?平面ABCD所以FD⊥CM.在矩形ABCD中,CD=2a,AD=a,M为AB的中点,DM=CM=
a所以CM⊥DM.进而根据线面垂直的判定定理可得线面垂直.
(Ⅱ)点P在A点处.取DC中点S,连接AS、GS、GA.因为G是DF的中点,GS∥FC,AS∥CM所以面GSA∥面FMC,根据面面平行的性质定理可得GP∥平面FMC
| 2 |
(Ⅱ)点P在A点处.取DC中点S,连接AS、GS、GA.因为G是DF的中点,GS∥FC,AS∥CM所以面GSA∥面FMC,根据面面平行的性质定理可得GP∥平面FMC
解答:解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC
(Ⅰ)∵直线FD⊥平面ABCD,CM?平面ABCD
∴FD⊥CM
在矩形ABCD中,CD=2a,AD=a,M为AB的中点,DM=CM=
a
∴CM⊥DM
又因为DM∩FD=D,FD?平面FDM,DM?平面FDM
∴CM⊥平面FDM
(Ⅱ)点P在A点处.
证明:取DC中点S,连接AS、GS、GA
∵G是DF的中点,GS∥FC,AS∥CM
∴面GSA∥面FMC,而GA?面GSA,
∴GP∥平面FMC
(Ⅰ)∵直线FD⊥平面ABCD,CM?平面ABCD
∴FD⊥CM
在矩形ABCD中,CD=2a,AD=a,M为AB的中点,DM=CM=
| 2 |
∴CM⊥DM
又因为DM∩FD=D,FD?平面FDM,DM?平面FDM
∴CM⊥平面FDM
(Ⅱ)点P在A点处.
证明:取DC中点S,连接AS、GS、GA
∵G是DF的中点,GS∥FC,AS∥CM
∴面GSA∥面FMC,而GA?面GSA,
∴GP∥平面FMC
点评:解决线面垂直的方法是在平面内找到两条相交直线与已知直线垂直即可,解决探索性问题最有效的方法是找特殊点如端点与线段的中点处,也可以利用空间向量解决此类问题.

练习册系列答案
相关题目
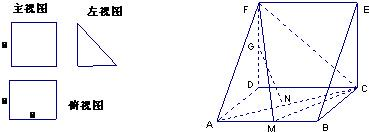 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.