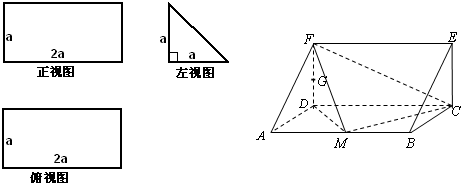
题目内容
一个多面体的直观图和三视图如图所示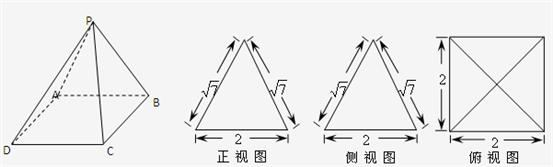
(1)求证:PA⊥BD;
(2)是否在线段PD上存在一Q点,使二面角Q-AC-D的平面角为30°,设λ=
| DQ | DP |
分析:(1)由已知中的三视图可知P-ABCD为一个底面棱长为2,侧高为
的正四棱锥,连接连接AC,BD交于点O,连接PO,由正方形的性质及O为顶点在底面上的射影,易结合线面垂直的判定定理得到BD⊥平面PAC,进而由线面垂直的性质,得到BD⊥PA;
(2)由AC⊥OQ,AC⊥OD,所以∠DOQ为二面角Q-AC-D的平面角,再根据二面角Q-AC-D的平面角为30°,我们易求出满足条件 的DQ的长,进而求出λ的值.
| 7 |
(2)由AC⊥OQ,AC⊥OD,所以∠DOQ为二面角Q-AC-D的平面角,再根据二面角Q-AC-D的平面角为30°,我们易求出满足条件 的DQ的长,进而求出λ的值.
解答:证明:(1)由三视图可知P-ABCD为四棱锥,底面ABCD为正方形,且PA=PB=PC=PD
连接AC,BD交于点O,连接PO,
因为BD⊥AC,BD⊥PO,所以BD⊥平面PAC,
即BD⊥PA;(6分)
解:(2)由三视图可知,BC=2,PA=2
,假设存在这样的D点
因为AC⊥OQ,AC⊥OD,所以∠DOQ为二面角Q-AC-D的平面角,(8分)
△PDO中,PD=2
,OD=
,则∠PDO=60°,△DQO中,∠PDO=60°,且∠QOD=30°.
所以DP⊥OQ,所以OD=
,QD=
(11分)
λ=
=
(12分)
连接AC,BD交于点O,连接PO,
因为BD⊥AC,BD⊥PO,所以BD⊥平面PAC,
即BD⊥PA;(6分)
解:(2)由三视图可知,BC=2,PA=2
| 2 |
因为AC⊥OQ,AC⊥OD,所以∠DOQ为二面角Q-AC-D的平面角,(8分)
△PDO中,PD=2
| 2 |
| 2 |
所以DP⊥OQ,所以OD=
| 2 |
| ||
| 2 |
λ=
| DQ |
| DP |
| 1 |
| 4 |
点评:本题考查的知识点是二面角的平面角及求法,由三视图还原实物图,其中(1)的关键是从已知的三视图中分析出棱锥的形状,(2)的关键是找出二面角Q-AC-D的平面角,再根据已知求出满足条件的DQ的长.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
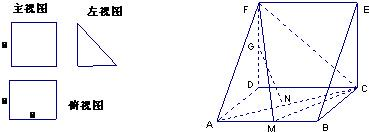 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.